---

\(a\) を正の整数とする. 正の実数 \(x\) についての方程式 \[ \text{(＊)} \quad x = \left[ \dfrac{1}{2} \left( x + \dfrac{a}{x} \right) \right] \] が解を持たないような \(a\) を小さい順に並べたものを \(a _ 1 , a _ 2 , a _ 3 , \cdots\) とする. ここに \([ ]\) はガウス記号で, 実数 \(u\) に対し, \([ u ]\) は \(u\) 以下の最大の整数を表す.

1. (1)　\(a = 7 , 8 , 9\) の各々について (＊) の解があるかどうかを判定し, ある場合は解 \(x\) を求めよ.

2. (2)　\(a _ 1 , a _ 2\) を求めよ.

3. (3)　\(\textstyle\sum\limits _ {n=1}^{\infty} \dfrac{1}{a _ n}\) を求めよ.

---

【 解 答 】

(＊) より, \(x\) は自然数である. また \[\begin{align} x & \leqq \dfrac{1}{2} \left( x +\dfrac{a}{x} \right) \lt x+1 \\ 2x^2 & \leqq x^2 +a \lt 2x^2+2x \quad ( \ \text{∵} \ x \gt 0 ) \\ x^2 -a & \leqq 0 , \ x^2 +2x -a \gt 0 \\ 0 \lt & x \leqq \sqrt{a} , \ x \gt -1+\sqrt{a+1} \quad ( \ \text{∵} \ a \gt 0 ) \\ \text{∴} \quad & \sqrt{a+1} -1 \lt x \leqq \sqrt{a} \quad ... [1] \end{align}\] ここで \(k\) を自然数とすると,

• \(k^2-1 \leqq a \lt ( k+1 )^2 -1\) のとき \[ k-1 \leqq \sqrt{a+1} -1 \lt k \]

• \(k^2 \leqq a \lt ( k+1 )^2\) のとき \[ k \leqq \sqrt{a} \lt k+1 \]

であることから

1. 1*　\(a = k^2-1\) のとき
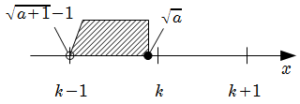   \(\sqrt{a+1} -1 = k-1\) , \(\sqrt{a} \lt k\) なので, [1] は自然数解をもたない.

2. 2*　\(k^2 \leqq a \lt ( k+1 )^2-1\) のとき
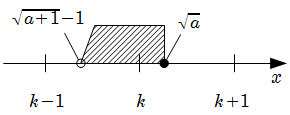   \(\sqrt{a+1} -1 \lt k , \ \sqrt{a} \geqq k\) なので, [1] の自然数解は \[ x = k \]

1* 2*より

• \(a=7\) のときは, \(\underline{x=2}\)

• \(a=8\) のときは,解なし

• \(a=9\) のときは, \(\underline{x=3}\)

(2)

(1) での考察より, \(a = k^2-1\) と表されるとき, (＊) は解を持たないので \[ a _ n = (n+1)^2-1 =n(n+2) \quad ... [2] \] ゆえに \[ a _ 1 = 1 \cdot 3 =\underline{3} , \ a _ 2 = 2 \cdot 4 =\underline{8} \]

(3)

[2] を用いれば \[\begin{align} \textstyle\sum\limits _ {n=1}^{\infty} \dfrac{1}{a _ n} & = \displaystyle\lim _ {m \rightarrow \infty} \textstyle\sum\limits _ {n=1}^{m} \dfrac{1}{n(n+2)} \\ & = \displaystyle\lim _ {m \rightarrow \infty} \textstyle\sum\limits _ {n=1}^{m} \dfrac{1}{2} \left( \dfrac{1}{n} -\dfrac{1}{n+2} \right) \\ & = \displaystyle\lim _ {m \rightarrow \infty} \dfrac{1}{2} \left( 1 +\dfrac{1}{2} -\dfrac{1}{m+1} -\dfrac{1}{m+2} \right) \\ & = \underline{\dfrac{3}{4}} \end{align}\]