\(N\) を正の整数とする. \(2N\) 以下の正の整数 \(m\) , \(n\) からなる組 \((m, n)\) で, 方程式 \(x^2-nx+m=0\) が \(N\) 以上の実数解をもつようなものは何組あるか.
【 解 答 】
条件より \[ 1 \leqq m \leqq 2N , \ 1 \leqq n \leqq 2N \quad ... [1] \] \(f(x) = x^2 -nx +m\) とおく. \[ f(x) =\left( x -\dfrac{n}{2} \right)^2 -\dfrac{n^2}{4} +m \] [1] より, \(0 \lt \dfrac{n}{2} \leqq N\) なので, \(f(x)=0\) が \(N\) 以上の実数解をもつ条件は \[\begin{align} f(N) & =N^2 -nN +m \leqq 0 \\ \text{∴} \quad m & \leqq Nn -N^2 \quad ... [2] \end{align}\] ゆえに, [1] [2] を満たす領域に含まれる格子点の個数を求めればよい.
1* \(N = 1\) のとき
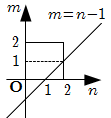 条件を満たす点は \(( 2 , 1 )\) のみで, \(1\) 個.
条件を満たす点は \(( 2 , 1 )\) のみで, \(1\) 個.2* \(N \geqq 2\) のとき
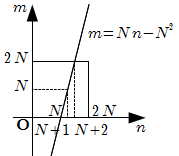 条件を満たす点は,
条件を満たす点は,
\(m = N+1\) 上に, \(N\) 個
\(m = k \ ( N+2 \leqq k \leqq N^2 )\) 上に, \(2N\) 個ずつ 存在するので \[ N +2N (N-1) = 2N^2-N \ \text{個} \]
以上より, 求める組数は \[ \underline{2N^2-N} \]
 条件を満たす点は \(( 2 , 1 )\) のみで, \(1\) 個.
条件を満たす点は \(( 2 , 1 )\) のみで, \(1\) 個.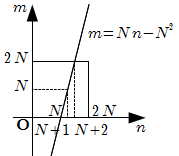 条件を満たす点は,
条件を満たす点は,