一辺の長さが \(1\) の正八角形 \(A _ 1 A _ 2 \cdots A _ 8\) の周上を \(3\) 点 \(P , Q , R\) が動くとする.
(1) \(\triangle PQR\) の面積の最大値を求めよ.
(2) \(Q\) が正八角形の頂点 \(A _ 1\) に一致し, \(\angle PQR = 90^{\circ}\) となるとき \(\triangle PQR\) の面積の最大値を求めよ.

【 解 答 】
(1)
まず点 \(P\) の位置について考えると, 辺 \(QR\) に平行な直線 \(\ell\) が正八角形と共有点をもつように動かして, 辺 \(QR\) から最も離れているとき, \(\triangle PQR\) の面積は最大になる.
これは, 点 \(P\) がある頂点に一致している場合である.
他の \(2\) 点 \(Q , R\) についても同様のことが成立するので, \(\triangle PQR\) が最大になるのは \(3\) 点 \(P , Q , R\) がすべていずれかの頂点に一致するときである.
したがって, 最大値をとる候補となる \(\triangle PQR\) は下図の [1] ~ [4] の場合である.
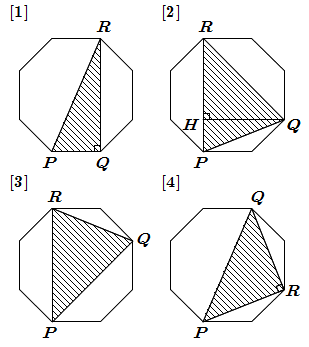
- [1] のとき \[ PR = 1 +2 \cdot \dfrac{\sqrt{2}}{2} = 1 +\sqrt{2} \] なので \[\begin{align} \triangle PQR & = \dfrac{1}{2} \cdot 1 \left( 1 +\sqrt{2} \right) \\ & = \dfrac{1 +\sqrt{2}}{2} \end{align}\]
- [2] のとき \[\begin{align} PR & = 1 +\sqrt{2} \\ QH & = 1 +\dfrac{\sqrt{2}}{2} = \dfrac{2 +\sqrt{2}}{2} \end{align}\] なので \[\begin{align} \triangle PQR & = \dfrac{1}{2} \left( 1 +\sqrt{2} \right) \cdot \dfrac{2 +\sqrt{2}}{2} \\ & = \dfrac{4 +3 \sqrt{2}}{4} \end{align}\]
- [3] のとき [2] のときと同じ三角形なので, \[ \triangle PQR = \dfrac{4 +3 \sqrt{2}}{4} \]
- [4] のとき \[\begin{align} PR & = QR = \sqrt{1^2 +1^2 -2 \cdot 1 \cdot 1 \cdot \sin 135^{\circ}} \\ & = \sqrt{2 +\sqrt{2}} \end{align}\] なので \[\begin{align} \triangle PQR & = \dfrac{1}{2} \left( \sqrt{2 +\sqrt{2}} \right)^2 \\ & = \dfrac{2 +\sqrt{2}}{2} \end{align}\]
以上より, 面積の最大値は \[ \underline{\dfrac{4 +3 \sqrt{2}}{4}} \]
(2)
\(QP , QR\) の延長線と正八角形の外接円の交点をそれぞれ \(P' , R'\) とおく.
\(\angle PQR = 90^{\circ}\) となるのは, \(P'R'\) が外接円の直径となるときである.
また
\[
\triangle PQR \leqq \triangle PQ'R' \quad ... [5]
\]
等号成立は, \(P=P' , \ R=R'\) のときである.
さらに
\[
\triangle PQ'R' \leqq \triangle A _ {1}A _ {3}A _ {7}
\]
等号成立は, \(P=A _ {3} , \ R=A _ {7}\) のときで, これは [5] の等号成立の条件も満たしている.
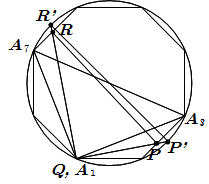
これは, (1) の [4] のときと同じ三角形なので, 求める面積の最大値は \[ \underline{\dfrac{2 +\sqrt{2}}{2}} \]