座標空間において, \(xy\) 平面内で不等式 \(|x| \leqq 1\) , \(|y| \leqq 1\) により定まる正方形 \(S\) の \(4\) つの頂点を A \(( -1, 1, 0 )\) , B \(( 1, 1, 0 )\) , C \(( 1, -1, 0 )\) , D \(( -1, -1, 0 )\) とする. 正方形 \(S\) を, 直線 BD を軸として回転させてできる立体を \(V _ 1\) , 直線 AC を軸として回転させてできる立体を \(V _ 2\) とする.
(1) \(0 \leqq t \lt 1\) を満たす実数 \(t\) に対し, 平面 \(x=t\) による \(V _ 1\) の切り口の面積を求めよ.
(2) \(V _ 1\) と \(V _ 2\) の共通部分の体積を求めよ.
【 解 答 】
(1)
立体 \(V _ 1\) は, AC を直径とする円が底面で頂点がそれぞれ B , D である \(2\) つの円すいを合わせた形である.
対称性から \(z \geqq 0\) の部分について考えればよい.
立体 \(V _ 1\) の表面上の点 P \(( t , s , z )\) ( \(0 \leqq t \lt 1\) ),
P から \(xy\) 平面に下ろした垂線の足を Q \(( t , s , 0 )\) , PQ に含み底面に平行な円すいの切り口の中心を R とおく.
1* \(s \geqq -t\) のとき
直線 QR は直線 AC と平行なので \[ \text{QR} : \quad x+y = t+s \] 点 R は, 直線 \(y=x\) 上の点なので \[ \text{Q} \ \left( \dfrac{t+s}{2} , \dfrac{t+s}{2} , 0 \right) \] したがって \[\begin{align} \text{RQ} & = \sqrt{2} \left( t -\dfrac{t+s}{2} \right) \\ & = \dfrac{t-s}{\sqrt{2}} \quad ...[1] \end{align}\] また \[\begin{align} \text{BO} : \text{BR} & = 1 : \left( 1 -\dfrac{t+s}{2} \right) \\ & = 2 : 2-(t+s) \end{align}\] なので, 相似である円すいに着目すれば \[\begin{align} \text{PR} & = \sqrt{2} \cdot \dfrac{2-(t+s)}{2} \\ & = \dfrac{2-(t+s)}{\sqrt{2}} \quad ...[2] \end{align}\] \(\text{PQ} = z\) なので, [1] [2] と三平方の定理より \[\begin{align} z & = \sqrt{\left( \dfrac{2-(t+s)}{\sqrt{2}} \right)^2 -\left( \dfrac{t-s}{\sqrt{2}} \right)^2} \\ & = \dfrac{\sqrt{2}}{2} \sqrt{(2-2s)(2-2t)} \\ & = \sqrt{2(1-t)} \sqrt{1-s} \end{align}\]2* \(s \lt -t\) のとき
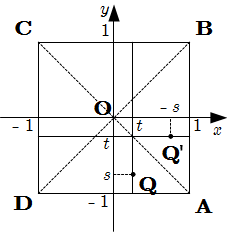 立体 \(V _ 1\) を構成する \(2\) つの円すいが平面 \(y = -x\) について対称であることから,
点Q' \(( -s , -t , 0 )\) を点 Q とみなして, 1*と同様に考えればよく
\[
z = \sqrt{2(1+t)} \sqrt{1+s}
\]
立体 \(V _ 1\) を構成する \(2\) つの円すいが平面 \(y = -x\) について対称であることから,
点Q' \(( -s , -t , 0 )\) を点 Q とみなして, 1*と同様に考えればよく
\[
z = \sqrt{2(1+t)} \sqrt{1+s}
\]
1*~2* より, 平面 \(x=t\) による立体 \(V _ 1\) の切り口は下図斜線部のようになる.
 よって, 求める面積を \(S _ t\) とおけば
\[\begin{align}
S _ t & = 2 \displaystyle\int _ {-1}^{-t} \sqrt{2(1+t)} \sqrt{1+y} \, dy \\ & \qquad +2 \displaystyle\int _ {-t}^{1} \sqrt{2(1-t)} \sqrt{1-y} \, dy \\
& = 2 \sqrt{2(1+t)} \left[ \dfrac{2}{3} (1+y)^{\frac{3}{2}} \right] _ {-1}^{-t} \\ & \qquad +2 \sqrt{2(1-t)} \left[ -\dfrac{2}{3} (1-y)^{\frac{3}{2}} \right] _ {-t}^{1} \\
& = \dfrac{4}{3} \sqrt{2(1+t)} (1-t)^{\frac{3}{2}} \\ & \qquad +\dfrac{4}{3} \sqrt{2(1-t)} (1+t)^{\frac{3}{2}} \\
& = \dfrac{4}{3} \sqrt{2 (1-t^2)} \left\{ (1-t)+(1+t) \right\} \\
& = \underline{\dfrac{8}{3} \sqrt{2 (1-t^2)}}
\end{align}\]
よって, 求める面積を \(S _ t\) とおけば
\[\begin{align}
S _ t & = 2 \displaystyle\int _ {-1}^{-t} \sqrt{2(1+t)} \sqrt{1+y} \, dy \\ & \qquad +2 \displaystyle\int _ {-t}^{1} \sqrt{2(1-t)} \sqrt{1-y} \, dy \\
& = 2 \sqrt{2(1+t)} \left[ \dfrac{2}{3} (1+y)^{\frac{3}{2}} \right] _ {-1}^{-t} \\ & \qquad +2 \sqrt{2(1-t)} \left[ -\dfrac{2}{3} (1-y)^{\frac{3}{2}} \right] _ {-t}^{1} \\
& = \dfrac{4}{3} \sqrt{2(1+t)} (1-t)^{\frac{3}{2}} \\ & \qquad +\dfrac{4}{3} \sqrt{2(1-t)} (1+t)^{\frac{3}{2}} \\
& = \dfrac{4}{3} \sqrt{2 (1-t^2)} \left\{ (1-t)+(1+t) \right\} \\
& = \underline{\dfrac{8}{3} \sqrt{2 (1-t^2)}}
\end{align}\]
(2)
立体 \(V _ 1\) と \(V _ 2\) の共通部分を立体 \(V\) とおく.
 立体 \(V _ 2\) についても (1) と同様に考えると, 点 Q' \(( t , -s , 0 )\) を点 Q とみなして考えればよい.
立体 \(V _ 2\) についても (1) と同様に考えると, 点 Q' \(( t , -s , 0 )\) を点 Q とみなして考えればよい.
したがって, 平面 \(x=t\) による立体 \(V _ 2\) の切り口は, 立体 \(V _ 1\) の切り口に対して \(z\) 軸対称となる.
なので, 立体 \(V\) の平面 \(x=t\) による切り口は, 下図斜線部のようになる.
 この面積を \(T _ t\) とおけば
\[\begin{align}
T _ t & = 4 \displaystyle\int _ {-1}^{0} \sqrt{2(1-t)} \sqrt{1+y} \, dy \\
& = 4 \sqrt{2(1-t)} \left[ \dfrac{2}{3} (1+y)^{\frac{3}{2}} \right] _ {-1}^{0} \\
& = \dfrac{8}{3} \sqrt{2(1-t)}
\end{align}\]
よって, 立体 \(V\) が平面 \(x=0\) について対称であることも用いれば, 求める体積 \(W\) は
\[\begin{align}
W & = 2 \displaystyle\int _ {0}^{1} T _ t \, dt \\
& = \dfrac{16 \sqrt{2}}{3} \left[ -\dfrac{2}{3} (1-t)^{\frac{3}{2}} \right] _ {0}^{1} \\
& = \underline{\dfrac{32 \sqrt{2}}{9}}
\end{align}\]
この面積を \(T _ t\) とおけば
\[\begin{align}
T _ t & = 4 \displaystyle\int _ {-1}^{0} \sqrt{2(1-t)} \sqrt{1+y} \, dy \\
& = 4 \sqrt{2(1-t)} \left[ \dfrac{2}{3} (1+y)^{\frac{3}{2}} \right] _ {-1}^{0} \\
& = \dfrac{8}{3} \sqrt{2(1-t)}
\end{align}\]
よって, 立体 \(V\) が平面 \(x=0\) について対称であることも用いれば, 求める体積 \(W\) は
\[\begin{align}
W & = 2 \displaystyle\int _ {0}^{1} T _ t \, dt \\
& = \dfrac{16 \sqrt{2}}{3} \left[ -\dfrac{2}{3} (1-t)^{\frac{3}{2}} \right] _ {0}^{1} \\
& = \underline{\dfrac{32 \sqrt{2}}{9}}
\end{align}\]
 立体 \(V _ 1\) を構成する \(2\) つの円すいが平面 \(y = -x\) について対称であることから,
点Q' \(( -s , -t , 0 )\) を点 Q とみなして, 1*と同様に考えればよく
\[
z = \sqrt{2(1+t)} \sqrt{1+s}
\]
立体 \(V _ 1\) を構成する \(2\) つの円すいが平面 \(y = -x\) について対称であることから,
点Q' \(( -s , -t , 0 )\) を点 Q とみなして, 1*と同様に考えればよく
\[
z = \sqrt{2(1+t)} \sqrt{1+s}
\]