\(-\dfrac{\pi}{2} \leqq x \leqq \dfrac{\pi}{2}\) における \(\cos x +\dfrac{\sqrt{3}}{4} x^2\) の最大値を求めよ. ただし, \(\pi \gt 3.1\) および \(\sqrt{3} \gt 1.7\) が成り立つことは証明なしに用いてよい.
【 解 答 】
\(f(x) = \cos x +\dfrac{\sqrt{3}}{4} x^2\) とおく.
\[
f(-x) = \cos x +\dfrac{\sqrt{3}}{4} x^2 = f(x)
\]
なので, \(0 \leqq x \leqq \dfrac{\pi}{2}\) について調べればよい.
\(f(x)\) を微分すると
\[
f'(x) = -\sin x +\dfrac{\sqrt{3}}{2} x
\]
\(f'(x) = 0\) を変形すると
\[
\dfrac{\sqrt{3}}{2} x = \sin x \quad ... [1]
\]
ここで
\[\begin{align}
\dfrac{\sqrt{3}}{2} \cdot \dfrac{\pi}{2} & \gt \dfrac{1.7 \cdot 3.1}{4} \\
& = \dfrac{5.27}{4} \gt 1
\end{align}\]
なので, [1] の両辺のグラフを比較すると下図のようになり,
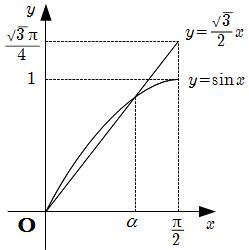
\(f'(x) = 0\) は, \(0 \lt x \lt \dfrac{\pi}{2}\) に解 \(x = \alpha\) を1つだけもつ.
したがって, \(f(x)\) の \(0 \leqq x \leqq \dfrac{\pi}{2}\) における増減は下表のようになる.
\[
\begin{array}{c|ccccc} x & 0 & \cdots & \alpha & \cdots & \dfrac{\pi}{2} \\ \hline f'(x) & 0 & - & 0 & + & \\ \hline f(x) & 1 & \searrow & \text{最小} & \nearrow & \dfrac{\sqrt{3} {\pi}^2}{16} \end{array}
\]
ここで
\[\begin{align}
\dfrac{\sqrt{3} {\pi}^2}{16} & \gt \dfrac{1.7 \cdot {3.1}^2}{16} \\
& = \dfrac{16.337}{16} \gt 1
\end{align}\]
よって, 求める最大値は \(x = \pm \dfrac{\pi}{2}\) のとき
\[
\underline{\dfrac{\sqrt{3} {\pi}^2}{16}}
\]