\(xy\) 平面上で, \(2\) 次曲線 \(C : \ x^2+ay^2+by = 0\) が直線 \(L : \ y = 2x-1\) に点 P で接している. ただし, \(a \neq -\dfrac{1}{4}\) とする.
(1) \(a\) と \(b\) の関係式を求めよ.
(2) \(C\) が楕円, 放物線, 双曲線となるそれぞれの場合に, \(b\) の値の範囲を求めよ.
(3) \(C\) が楕円とする場合の接点Pの存在範囲を求め, \(xy\) 平面上に図示せよ.
【 解 答 】
(1)
\(b = 0\) のとき, \(C\) は \(2\) 次曲線を表さないので \[ b \neq 0 \quad ... [1] \] 以下では, [1] のもとで考える. \(L\) の式より \[ x = \dfrac{y+1}{2} \] これを \(C\) の式に代入すると \[\begin{align} (y+1)^2 +4ay^2 +4by & = 0 \\ \text{∴} \quad (4a+1) y^2 +2(2b+1) y +1 & = 0 \quad ... [2] \end{align}\] \(a \neq -\dfrac{1}{4}\) なので, [2] は \(y\) の \(2\) 次方程式であり, これが重解をもつので, 判別式 \(D\) について \[\begin{align} \dfrac{D}{4} = (2b+1)^2 -(4a+1) & = 0 \\ b^2 +b -a & = 0 \\ \text{∴} \quad a & = b(b+1) \end{align}\] ただし, \(a \neq -\dfrac{1}{4}\) より \[\begin{align} b^2 +b +\dfrac{1}{4} & = \left( b+\dfrac{1}{2} \right)^2 \neq 0 \\ \text{∴} \quad b & \neq -\dfrac{1}{2} \end{align}\] また, \(b = 0\) の場合は除くので \[ (a,b) \neq (0,0) \] 以上より, \(a ,b\) の関係は \[ \underline{a = b(b+1) \ \left( (a,b) \neq (0,0) , \left( -\dfrac{1}{4} , -\dfrac{1}{2} \right) \right)} \]
(2)
\(C\) は
\(a \gt 0\) のとき, 楕円
\(a = 0\) のとき, 放物線
\(a \lt 0\) のとき, 双曲線
なので, (1) の結果より \[ \underline{\left\{ \begin{array}{ll} \text{楕円} : & b \lt -1 , \ 0 \lt b \\ \text{放物線} : & b = -1 \\ \text{双曲線} : & -1 \lt b \lt -\dfrac{1}{2} , -\dfrac{1}{2} \lt b \lt 0 \end{array} \right.} \]
(3)
(1) の結果を [2] に代入すると \[\begin{align} (2b+1)^2 y^2+2(2b+1)y +1 & = 0 \\ \left\{ (2b+1)y +1 \right\}^2 & = 0 \\ \text{∴} \quad y = -\dfrac{1}{2b+1} & \end{align}\] これは, 点 P の \(y\) 座標であり, \(-1 \lt b , 0 \lt b\) で取り得る値の範囲は
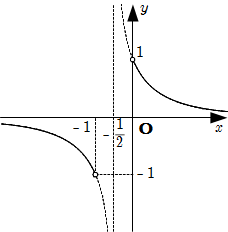
\[ -1 \lt y \lt 0 , \ 0 \lt y \lt 1 \] よって, P の軌跡は \[ y = 2x-1 \quad ( -1 \lt y \lt 0 , 0 \lt y \lt 1 ) \] 図示すると下図実線部(○は除く).