\(xyz\) 空間内において, \(yz\) 平面上で放物線 \(z = y^2\) と直線 \(z = 4\) で囲まれる平面図形を \(D\) とする. 点 \(( 1, 1, 0 )\) を通り \(z\) 軸に平行な直線を \(\ell\) とし, \(\ell\) のまわりに \(D\) を \(1\) 回転させてできる立体を \(E\) とする.
(1) \(D\) と平面 \(z=t\) との交わりを \(D _ t\) とする. ただし \(0 \leqq t \leqq 4\) とする. 点Pが \(D _ t\) 上を動くとき, 点Pと点 \(( 1, 1, t )\) との距離の最大値, 最小値を求めよ.
(2) 平面 \(z=t\) による \(E\) の切り口の面積 \(S(t) \ ( 0 \leqq t \leqq 4 )\) を求めよ.
(3) \(E\) の体積 \(V\) を求めよ.
【 解 答 】
(1)
\[ D _ t : \ x = 0 , \ z = t \quad \left( -\sqrt{t} \leqq y \leqq \sqrt{t} \right) \] なので, 場合分けして考える.
1* \(0 \leqq t \leqq 1\) のとき
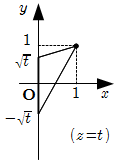 最大値 \(R _ t\) は
\[
R _ t = \sqrt{\left( 1+\sqrt{t} \right)^2 +1} = \sqrt{t +2\sqrt{t} +2}
\]
最小値 \(r _ t\) は
\[
r _ t = \sqrt{\left( 1-\sqrt{t} \right)^2 +1} = \sqrt{t -2\sqrt{t} +2}
\]
最大値 \(R _ t\) は
\[
R _ t = \sqrt{\left( 1+\sqrt{t} \right)^2 +1} = \sqrt{t +2\sqrt{t} +2}
\]
最小値 \(r _ t\) は
\[
r _ t = \sqrt{\left( 1-\sqrt{t} \right)^2 +1} = \sqrt{t -2\sqrt{t} +2}
\]2* \(1 \lt t \leqq 4\) のとき
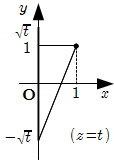 最大値 \(R _ t\) は, 1* のときと同様に
\[
R _ t = \sqrt{t +2\sqrt{t} +2}
\]
最小値 \(r _ t\) は
\[
r _ t = 1
\]
最大値 \(R _ t\) は, 1* のときと同様に
\[
R _ t = \sqrt{t +2\sqrt{t} +2}
\]
最小値 \(r _ t\) は
\[
r _ t = 1
\]
以上より, 最大値は \[ R _ t = \underline{\sqrt{t +2\sqrt{t} +2}} \] 最小値は \[ r _ t =\underline{\left\{ \begin{array}{ll} \sqrt{t -2\sqrt{t} +2} & \ \left( \ 0 \leqq t \leqq 1 \text{のとき} \right) \\ 1 & \ \left( \ 0 \leqq t \leqq 4 \text{のとき} \right) \end{array} \right.} \]
(2)
\[ S(t) = \pi {R _ t}^2 -\pi {r _ t}^2 = \pi \left( {R _ t}^2 -{r _ t}^2 \right) \] なので, (1) の結果より \[ S(t) = \underline{\left\{ \begin{array}{ll} 4 \pi \sqrt{t} & \ \left( \ 0 \leqq t \leqq 1 \text{のとき} \right) \\ \pi \left( \sqrt{t}+1 \right)^2 & \ \left( \ 0 \leqq t \leqq 4 \text{のとき} \right) \end{array} \right.} \]
(3)
\[\begin{align} V & = \displaystyle\int _ 0^4 S(t) \, dt \\ & = 4 \pi \displaystyle\int _ 0^1 \sqrt{t} \, dt +\pi \displaystyle\int _ 1^4 \left( t +2\sqrt{t}+1 \right) \, dt \\ & = 4 \pi \left[ \dfrac{2 t^{\frac{3}{2}}}{3} \right] _ 0^1 +\pi \left[ \dfrac{t^2}{2} +\dfrac{4 t^{\frac{3}{2}}}{3} +t \right] _ 1^4 \\ & = \dfrac{8 \pi}{3} +\pi \left( 8 +\dfrac{32}{3} +4 \right) -\pi \left( \dfrac{1}{2} +\dfrac{4}{3} +1 \right) \\ & = \underline{\dfrac{45 \pi}{2}} \end{align}\]
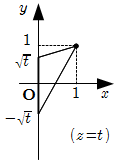 最大値 \(R _ t\) は
\[
R _ t = \sqrt{\left( 1+\sqrt{t} \right)^2 +1} = \sqrt{t +2\sqrt{t} +2}
\]
最小値 \(r _ t\) は
\[
r _ t = \sqrt{\left( 1-\sqrt{t} \right)^2 +1} = \sqrt{t -2\sqrt{t} +2}
\]
最大値 \(R _ t\) は
\[
R _ t = \sqrt{\left( 1+\sqrt{t} \right)^2 +1} = \sqrt{t +2\sqrt{t} +2}
\]
最小値 \(r _ t\) は
\[
r _ t = \sqrt{\left( 1-\sqrt{t} \right)^2 +1} = \sqrt{t -2\sqrt{t} +2}
\] 最大値 \(R _ t\) は, 1* のときと同様に
\[
R _ t = \sqrt{t +2\sqrt{t} +2}
\]
最小値 \(r _ t\) は
\[
r _ t = 1
\]
最大値 \(R _ t\) は, 1* のときと同様に
\[
R _ t = \sqrt{t +2\sqrt{t} +2}
\]
最小値 \(r _ t\) は
\[
r _ t = 1
\]