平面上の鋭角三角形 △ABC の内部(辺や頂点は含まない)に点 P をとり, A' を B, C, P を通る円の中心, B' を C, A, P を通る円の中心, C' を A, B, P を通る円の中心とする. このとき A, B, C, A', B', C' が同一円周上にあるための必要十分条件は P が △ABC の内心に一致することであることを示せ.
【 解 答 】
- [P] : 「 A, B, C, A', B', C' が同一円周上にある. 」
- [Q] : 「 P が △ABC の内心である. 」
\(\angle \text{A} =2a\) , \(\angle \text{B} =2b\) , \(\angle \text{C} =2c\) とおくと \[ a+b+c = \dfrac{\pi}{2} \quad ... [1] \]
\([ \text{Q} ] \Rightarrow [ \text{P} ]\) の証明
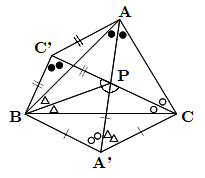
P は △ABC の内心なので \[ \angle \text{PAB} = a , \ \angle \text{PBC} = b , \ \angle \text{PCB} = c \] A, B, P は C' を中心とする円周上の点なので \[\begin{align} \angle \text{BC'P} & = 2a \quad ... [2] \\ \text{∴} \quad \angle \text{C'PB} & =\dfrac{\pi -2a}{2} = \dfrac{\pi}{2} -a \quad ... [3] \end{align}\] B, C, P は A' を中心とする円周上の点なので, 同様に \[\begin{align} \angle \text{PA'B} & = 2c , \ \angle \text{PA'C} = 2b \\ \text{∴} \quad \angle \text{BPA'} & = \dfrac{\pi}{2} -b , \ \angle \text{CPA'} = \dfrac{\pi}{2} -c \quad ... [4] \end{align}\] [3] [4] を用いれば \[ \angle \text{CPC'} = \dfrac{3\pi}{2} - (a+b+c) = \pi \quad ( \ \text{∵} \ [1] \] したがって, Pは線分CC'上に存在する.
ゆえに, [2] より, \(\angle \text{BAC} = \angle \text{BC'C}\) なので, A, B, C, C'は同一円周上に存在する.
同様にすれば, B', A' も, A, B, C と同一円周上に存在することが示せる.
よって \[ [ \text{Q} ] \Rightarrow [ \text{P} ] \]\([ \text{P} ] \Rightarrow [ \text{Q} ]\) の証明
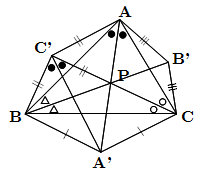
条件より, \(\text{A'B} =\text{A'C}\) , \(\text{B'C} =\text{B'A}\) , \(\text{C'A} =\text{C'B}\) なので \[\begin{align} \angle \text{BAA'} = \angle \text{CAA'} & , \ \angle \text{CBB'} = \angle \text{ABB'} , \\ \angle \text{BCC'} & = \angle \text{ACC'} \quad ... [5] \end{align}\] また, \(\angle \text{BC'A'} = \angle \text{CC'A'}\) すなわち
「 A'C' は \(\angle \text{BC'C}\) を \(2\) 等分する. 」 ... [6] 次に条件より, \(\text{BC'} =\text{PC'}\) , \(\text{BA'} =\text{PA'}\) なので
「 A'C' は \(\angle \text{BC'P}\) を \(2\) 等分する. 」 ... [7] したがって, [6] [7] より, P は線分 CC' 上に存在する.
同様にすれば
「 Pは線分AA', BB'上に存在する. 」 ... [8] [5] より, AA', BB', CC' は各頂角 A, B, C の \(2\) 等分線なので, 内心の一点で交わるが, [8] より, P が内心に他ならない.
よって \[ [ \text{P} ] \Rightarrow [ \text{Q} ] \]
以上より, 題意は示された.

