実数 \(a\) に対して, \(x\) の方程式 \[ | x(x-2) | +2a | x | -4a | x-2 | -1 = 0 \] が, 相異なる \(4\) つの実数解をもつような \(a\) の範囲を求めよ.

【 解 答 】

\[\begin{align} | x(x-2) | +2a | x | & -4a | x-2 | -1 = 0 \\ | x(x-2) | -1 & = 2a \left( 2 | x-2 | - | x | \right) \quad ... [1] \end{align}\] [1] の左辺と右辺をそれぞれ \(f(x)\) , \(g(x)\) とおくと \[\begin{align} f(x) & = \left\{ \begin{array}{ll} x^2 -2x -1 & \left( \ x \leqq 0 , 2 \leqq x \text{のとき} \right) \\ -x^2 +2x -1 & \ \left( \ 0 \lt x \lt 2 \text{のとき} \right) \end{array} \right. , \\ g(x) & = \left\{ \begin{array}{ll} 2a (-x+4) & \left( \ x \leqq 0 \text{のとき} \right) \\ 2a(-3x+4) & \left( \ 0 \lt x \lt 2 \text{のとき} \right) \\ 2a(x-4) & \left( \ x \geqq 2 \text{のとき} \right) \end{array} \right. \end{align}\]

1. 1*　\(x \leqq 0\) のとき 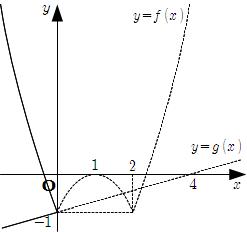\(y = g(x)\) は, 定点 \((4, 0)\) を通る傾き \(-2a\) の直線である.
   これが点 \((0, -1)\) を通るのは \[\begin{align} -2a & = \dfrac{1}{4} \\ \text{∴} \quad a & = -\dfrac{1}{8} \end{align}\] したがって, この範囲での [1] の実数解の個数は \[ \left\{ \begin{array}{ll} 0 & \left( \ a \lt -\dfrac{1}{8} \text{のとき} \right) \\ 1 & \left( \ a \geqq -\dfrac{1}{8} \text{のとき} \right) \end{array} \right. \]

2. 2*　\(0 \lt x \lt 2\) のとき 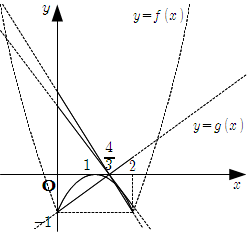\(y = g(x)\) は, 定点 \(\left( \dfrac{4}{3}, 0 \right)\) を通る傾き \(-6a\) の直線である.
   この直線が

   1. [A]　点 \((0 , -1)\) を通るのは \[\begin{align} -6a & = \dfrac{3}{4} \\ \text{∴} \quad a &= -\dfrac{1}{8} \end{align}\]

   2. [B]　点 \((2 , -1)\) を通るのは \[\begin{align} -6a & = -\dfrac{3}{2} \\ \text{∴} \quad a & = \dfrac{1}{4} \end{align}\]

   3. [C]　\(y=f(x)\) と接するのは, それぞれの式より \(y\) を消去して \[\begin{align} -x^2 +2x -1 & = 2a(-3x+4) \\ x^2 -2(3a+1)x +8a+1 & = 0 \quad ... [2] \end{align}\] [2] の判別式 \(D _ 1\) について \[\begin{align} \dfrac{D _ 1}{4} = (3a+1)^2 & -(8a+1) = 0 \\ a (9a-2) & = 0 \\ \text{∴} \quad a & = 0 , \dfrac{2}{9} \end{align}\] \(2\) つの解はともに [A] と [B] の場合の間に含まれるので, 接点は \(0 \lt x \lt 2\) の範囲にある.

   したがって, この範囲での [1] の実数解の個数は \[ \left\{ \begin{array}{ll} 1 & \left( \ a \leqq -\dfrac{1}{8} \text{のとき} \right) \\ 2 & \left( \ -\dfrac{1}{8} \lt a \lt 0 \text{のとき} \right) \\ 1 & \left( \ a=0 \text{のとき} \right) \\ 0 & \left( \ 0 \lt a \lt \dfrac{2}{9} \text{のとき} \right) \\ 1 & \left( \ a= \dfrac{2}{9} \text{のとき} \right) \\ 2 & \left( \ \dfrac{2}{9} \lt a \lt \dfrac{1}{4} \text{のとき} \right) \\ 1 & \left( \ a \geqq \dfrac{1}{4} \text{のとき} \right) \end{array} \right. \]

3. 3*　\(x \geqq 2\) のとき 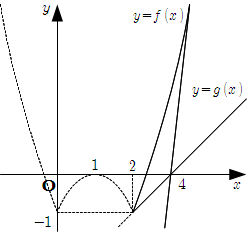\(y = g(x)\) は, 定点 \((4, 0)\) を通る傾き \(2a\) の直線である.
   この直線が

   1. [A]　点 \((2, -1)\) を通るのは \[\begin{align} 2a & = \dfrac{1}{2} \\ \text{∴} \quad a & = \dfrac{1}{4} \end{align}\]

   2. [B]　\(y=f(x)\) と接するのは, それぞれの式より \(y\) を消去して \[\begin{align} x^2 -2x -1 & = 2a(x-4) \\ x^2 -2(a+1)x +8a-1 & = 0 \quad ... [2] \end{align}\] [2] の判別式 \(D _ 2\) について \[\begin{align} \dfrac{D _ 2}{4} = (a+1)^2 & -(8a-1) = 0 \\ a^2 -6a +2 & = 0 \\ \text{∴} \quad a & = 3 \pm \sqrt{7} \end{align}\] このうち, 接点が \(x \geqq 2\) に含まれるのは, 傾きが大きい方なので \[ a = 3 +\sqrt{7} \]

   したがって, この範囲での [1] の実数解の個数は \[ \left\{ \begin{array}{ll} 1 & \left( \ a \leqq \dfrac{1}{4} \text{のとき} \right) \\ 0 & \left( \ \dfrac{1}{4} \lt a \lt 3+\sqrt{7} \text{のとき} \right) \\ 1 & \left( \ a = 3 +\sqrt{7} \text{のとき} \right) \\ 2 & \left( \ a \gt 3+\sqrt{7} \text{のとき} \right) \end{array} \right. \]

1*～3*の場合をまとめると, [1] の実数解の個数 \(N\) は下表のようになる. \[ \begin{array}{c|ccccccccccc} a & \cdots & -\frac{1}{8} & \cdots & 0 & \cdots & \frac{2}{9} & \cdots & \frac{1}{4} & \cdots & 3 +\sqrt{7} & \cdots \\ \hline \hline \mathbf{1^* } & 0 & 1 & 1 & 1 & 1 & 1 & 1 & 1 & 1 & 1 & 1 \\ \hline \mathbf{2^* } & 1 & 1 & 2 & 1 & 0 & 1 & 2 & 1 & 1 & 1 & 1 \\ \hline \mathbf{3^* } & 1 & 1 & 1 & 1 & 1 & 1 & 1 & 1 & 0 & 1 & 2 \\ \hline \hline N & 2 & 3 & 4 & 3 & 2 & 3 & 4 & 3 & 2 & 3 & 4 \end{array} \] よって, 求める \(a\) の範囲は \[ \underline{-\dfrac{1}{8} \lt a \lt 0 , \ \dfrac{2}{9} \lt a \lt \dfrac{1}{4} , \ 3+\sqrt{7} \lt a} \]