平面上に一辺の長さが \(1\) の正方形 \(D\) および \(D\) と交わる直線があるとする. この直線を軸に \(D\) を回転して得られる回転体について以下の問に答えよ.
(1) \(D\) と同じ平面上の直線 \(l\) は \(D\) のどの辺にも平行でないものとする. 軸とする直線は \(l\) と平行なものの中で考えるとき, 回転体の体積を最大にする直線は \(D\) と唯 \(1\) 点で交わることを示せ.
(2) \(D\) と交わる直線を軸としてできるすべての回転体の体積の中で最大となる値を求めよ.
【 解 答 】
(1)
図形 \(R\) は領域 \(0 \leqq x \leqq a\) にあり, 直線 \(x = k\) に含まれる部分の長さ(以後, 幅とよぶ)が \(f(k)\) であるとする.
このとき, 図形 \(R\) の \(y\) 軸を中心とした回転体の体積 \(V\) は
\[
V = 2\pi \displaystyle\int _ 0^a x f(x) dx
\]

以下では \(2\) つの補題 [A], [B] を示す.
補題 [A] :
\(2\) つの図形 \(R _ 1 , R _ 2\) はそれぞれ領域 \(0 \leqq x \leqq a , \ b \leqq x \leqq a+b\) にあり, 幅がそれぞれ \(f(x) , g(x)\) であるとする.
このとき, \(f(x+b) = g(x)\) であれば, 図形 \(R _ 1 , R _ 2\) の \(y\) 軸を中心にした回転体の体積をそれぞれ \(V _ 1 , V _ 2\) とすれば \[ V _ 1 \lt V _ 2 \]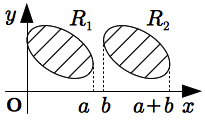
- [A] の証明:
\[\begin{align} V _ 1 & = 2\pi \displaystyle\int _ 0^a x f(x) dx \\ V _ 2 & = 2\pi \displaystyle\int _ b^{a+b} x f(x+b) dx \end{align}\] ここで \(u = x-b\) とおけば \[\begin{gather} dx = du , \\ \begin{array}{c|ccc} x & b & \rightarrow & a+b \\ \hline u & 0 & \rightarrow & a \end{array} \end{gather}\] ゆえに \[\begin{align} V _ 2 & = 2\pi \displaystyle\int _ 0^a (u+b) f(u) \, du \\ & = V _ 1 +2b\pi \displaystyle\int _ 0^a f(u) \, du \gt V _ 1 \end{align}\]
- [A] の証明:
補題 [B] :
図形 \(R\) は領域 \(0 \leqq x \leqq a\) にあり, 幅 \(f(x)\) が単調増加であるとする.
このとき, 図形領域 \(R\) の \(y\) 軸, 直線 \(x = a\) を中心にした回転体の体積をそれぞれ \(V _ 1 , V _ 2\) とすれば \[ V _ 1 \gt V _ 2 \]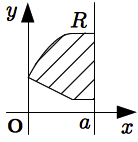
- [B] の証明:
\[\begin{align}
V _ 1 & = 2\pi \displaystyle\int _ 0^a x f(x) \, dx , \\
V _ 2 & = 2\pi \displaystyle\int _ 0^a x f(a-x) \, dx
\end{align}\]
なので
\[\begin{align}
\dfrac{V _ 1 -V _ 2}{2\pi} & = \displaystyle\int _ 0^a x \left\{ f(x) -f(a-x) \right\} \, dx \\
& = \displaystyle\int _ 0^{\frac{a}{2}} x \left\{ f(x) -f(a-x) \right\} \, dx \\
& \qquad +\underline{\displaystyle\int _ {\frac{a}{2}}^a x \left\{ f(x) -f(a-x) \right\} \, dx} _ {[1]}
\end{align}\]
下線部 [1] について, \(u = a-x\) とおけば
\[\begin{gather}
dx = -du , \\
\begin{array}{c|ccc} x & \dfrac{a}{2} & \rightarrow & a \\ \hline u & \dfrac{a}{2} & \rightarrow & 0 \end{array}
\end{gather}\]
ゆえに
\[\begin{align}
[1] & = \displaystyle\int _ 0^{\frac{a}{2}} (a-u) \left\{ f(a-u) -f(u) \right\} \, du \\
& = \displaystyle\int _ 0^{\frac{a}{2}} (u-a) \left\{ f(u) -f(a-u) \right\} \, du
\end{align}\]
したがって
\[
\dfrac{V _ 1 -V _ 2}{2\pi} = \displaystyle\int _ 0^{\frac{a}{2}} (a-2x) \left\{ f(a-x) -f(x) \right\} \, dx
\]
ここで, \(0 \leqq x \leqq \dfrac{a}{2}\) のとき, \(2x-a \geqq 0 \quad ... [1]\) .
また \(f(x)\) は単調増加なので, \(f(a-x) -f(x) \geqq 0 \quad ... [2]\) .
常に [1] [2] ともに等号成立することはないので \[\begin{align} \dfrac{V _ 1 -V _ 2}{2\pi} \gt 0 \\ \text{∴} \quad V _ 1 \gt V _ 2 \end{align}\]
- [B] の証明:
\[\begin{align}
V _ 1 & = 2\pi \displaystyle\int _ 0^a x f(x) \, dx , \\
V _ 2 & = 2\pi \displaystyle\int _ 0^a x f(a-x) \, dx
\end{align}\]
なので
\[\begin{align}
\dfrac{V _ 1 -V _ 2}{2\pi} & = \displaystyle\int _ 0^a x \left\{ f(x) -f(a-x) \right\} \, dx \\
& = \displaystyle\int _ 0^{\frac{a}{2}} x \left\{ f(x) -f(a-x) \right\} \, dx \\
& \qquad +\underline{\displaystyle\int _ {\frac{a}{2}}^a x \left\{ f(x) -f(a-x) \right\} \, dx} _ {[1]}
\end{align}\]
下線部 [1] について, \(u = a-x\) とおけば
\[\begin{gather}
dx = -du , \\
\begin{array}{c|ccc} x & \dfrac{a}{2} & \rightarrow & a \\ \hline u & \dfrac{a}{2} & \rightarrow & 0 \end{array}
\end{gather}\]
ゆえに
\[\begin{align}
[1] & = \displaystyle\int _ 0^{\frac{a}{2}} (a-u) \left\{ f(a-u) -f(u) \right\} \, du \\
& = \displaystyle\int _ 0^{\frac{a}{2}} (u-a) \left\{ f(u) -f(a-u) \right\} \, du
\end{align}\]
したがって
\[
\dfrac{V _ 1 -V _ 2}{2\pi} = \displaystyle\int _ 0^{\frac{a}{2}} (a-2x) \left\{ f(a-x) -f(x) \right\} \, dx
\]
ここで, \(0 \leqq x \leqq \dfrac{a}{2}\) のとき, \(2x-a \geqq 0 \quad ... [1]\) .
ここから, 題意を示す.
対称性から, 軸の位置は \(D\) の中心 O を通る直線より左側のみを考えればよい.
もっとも左の \(1\) 頂点を通る直線を \(L\) , その他の直線を \(K\) とおき, それぞれを中心にした \(D\) の回転体の体積を \(V _ L , V _ K\) とおく.
\(D\) が \(K\) によって分けられる部分の左側を \(A\) , 右側を \(B\) とおき, 各部分の, \(L , K\) を中心にした回転体の体積をそれぞれ \(V _ {LA}\) と \(V _ {LB}\) , \(V _ {KA}\) と \(V _ {KB}\) とおく.

このとき \[\begin{align} V _ L & = V _ {LA} +V _ {LB} \\ V _ K & \lt V _ {KA} +V _ {KB} \quad ( \ \text{∵} \ \text{回転体どうしに重なりがある} ) \end{align}\] 補題 [A] より \[ V _ {LB} \gt V _ {KB} \] 部分 \(A\) は右にいくほど軸方向の幅が単調増加しているので, 補題 [B] より \[ V _ {LA} \gt V _ {KA} \] 以上より \[ V _ L = V _ {LA} +V _ {LB} \gt V _ {KA} +V _ {KB} \gt V _ K \] よって, 題意は示された.
(2)

