\(3\) 次関数 \(y = x^3 -3x^2 +2x\) のグラフを \(C\) , 直線 \(y = ax\) を \(l\) とする.
(1) \(C\) と \(l\) が原点以外の共有点をもつような実数 \(a\) の範囲を求めよ.
(2) \(a\) が (1) で求めた範囲内にあるとき, \(C\) と \(l\) によって囲まれる部分の面積を \(S(a)\) とする. \(S(a)\) が最小となる \(a\) の値を求めよ.
【 解 答 】
(1)
\(C\) と \(l\) の式より \[\begin{align} x^3 -3x^2 +2x & = ax \\ \text{∴} \quad x \left( x^2 -3x +2 -a \right) & = 0 \end{align}\] したがって, \(x\) の方程式 \( x^2 -3x -a+2 = 0 \quad ... [1]\) が \(x = 0\) 以外に解をもつ条件を求めればよい.
1* [1] が \(x = 0\) を解にもつとき \[\begin{align} -a+2 & = 0 \\ \text{∴} \quad a & = 2 \end{align}\] このとき, [1] は \[\begin{align} x (x-3) & = 0 \\ \text{∴} \quad x & = 0 , 3 \end{align}\] なので, \(x = 0\) 以外の解をもつ.
2* \(a \neq 2\) ( [1] が \(x = 0\) を解にもたない)とき
[1] の判別式 \(D\) について \[\begin{align} D = 3^2 -4(2-a) & \geqq 0 \\ \text{∴} \quad a & \geqq -\dfrac{1}{4} \end{align}\]
以上より, 求める範囲は \[ \underline{a \geqq -\dfrac{1}{4}} \]
(2)
\(C\) と \(l\) によって囲まれる部分を \(R\) とおく.
\(C\) と \(l\) の交点の \(x\) 座標を \(0 , \alpha , \beta \ ( \alpha \leqq \beta )\) とおくと, [1] について, 解と係数の関係より
\[
\alpha +\beta = 3 , \ \alpha \beta = -a+2 \quad ... [2]
\]
[1] を解けば
\[
x = \dfrac{3 \pm \sqrt{3^2 -4(2-a)}}{2} = \dfrac{3 \pm \sqrt{4a+1}}{2}
\]
なので
\[
\alpha = \dfrac{3 -\sqrt{4a+1}}{2} , \ \beta = \dfrac{3 +\sqrt{4a+1}}{2}
\]
したがって
\[
\dfrac{d \beta}{da} = -\dfrac{d \alpha}{da} \quad ... [3]
\]
さらに, \(f(x) = x^3 -3x^2 +2x\) とおき, 原始関数のひとつ \(F(x)\) を
\[
F(x) =\displaystyle\int f(x) \, dx =\dfrac{x^4}{4} -x^3 +x^2
\]
とおく.
このとき
\[
f( \alpha ) -a \alpha =0 , \ f( \beta ) -a \beta =0 \quad ... [4]
\]
以下では, \(D\) の形状によって場合分けして考える.
1* \(-\dfrac{1}{4} \leqq a \leqq 2\) のとき
このとき, \(\alpha \beta \geqq 0\) なので \[ 0 \leqq \alpha \leqq \beta \] ゆえに \(R\) は下図のようになり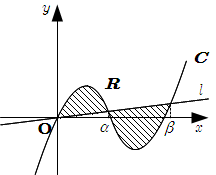
\[\begin{align} S(a) & = \displaystyle\int _ 0^{\alpha} \left( f(x) -ax \right) \, dx +\displaystyle\int _ {\alpha}^{\beta} \left( ax -f(x) \right) \, dx \\ & = F( \alpha ) -F(0) -\dfrac{a \alpha^2}{2} +\dfrac{a \beta^2}{2} -\dfrac{a \alpha^2}{2} -F( \beta ) +F( \alpha ) \\ & = 2F( \alpha ) -F( \beta ) -a \alpha^2 +\dfrac{a \beta^2}{2} \end{align}\] したがって \[\begin{align} S'(a) & = 2 f( \alpha ) \cdot \dfrac{d \alpha}{da} -f( \beta ) \cdot \dfrac{d \beta}{da} \\ & \qquad -\alpha^2 -a \cdot 2\alpha \cdot \dfrac{d \alpha}{da} +\dfrac{\beta^2}{2} +\dfrac{a}{2} \cdot 2 \beta \cdot \dfrac{d \beta}{da} \\ & = \left\{ 2 \left( f( \alpha ) -a \alpha \right) +f( \beta ) -a \beta \right\} \dfrac{d \alpha}{da} -\alpha^2 +\dfrac{\beta^2}{2} \quad ( \ \text{∵} \ [3] \ ) \\ & = -\alpha^2 +\dfrac{\beta^2}{2} \quad ( \ \text{∵} \ [4] \ ) \end{align}\] ここで, \(\alpha^2\) は \(a\) の単調減少関数, \(\beta^2\) は \(a\) の単調増加関数なので, \(S'(a)\) は \(a\) の単調増加関数である.
なので, \(S'(a) =0\) は高々 \(1\) つの解しかもたない.
これを解くと \[\begin{align} \alpha^2 & = \dfrac{\beta^2}{2} \\ \text{∴} \quad \beta & = \sqrt{2} \alpha \end{align}\] これを [2] に代入すれば \[\begin{align} \alpha & = \dfrac{3}{\sqrt{2} +1} =3 \left( \sqrt{2} -1 \right) , \\ a & = 2 -\sqrt{2} \alpha^2 =2 -9 \sqrt{2} \left( \sqrt{2} -1 \right)^2 \\ & = 38 -27 \sqrt{2} = -0.8 \cdots \end{align}\] したがって, \(S(a)\) の増減表は下のようになる. \[ \begin{array}{c|ccccc} a & -\frac{1}{4}& \cdots & 38 -27 \sqrt{2} & \cdots & 2 \\ \hline S'(a) & & - & 0 & + & \\ \hline S(a) & & \searrow & \text{最小} & \nearrow & \end{array} \]2* \(a \gt 2\) のとき
このとき, \(\alpha \beta \lt 0\) なので \[ \alpha \lt 0 \lt \beta \] ゆえに \(R\) は下図のようになる.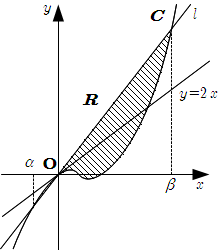
このとき, 明らかに \(S(a) \gt S(2)\) なので, この範囲で最小値をとることはない.
1* 2*より, \(S(a)\) を最小にする \(a\) の値は \[ a =\underline{38 -27 \sqrt{2}} \]

