空間内に平面 \(P\) がある. 空間内の図形 \(A\) に対し, \(A\) の各点から \(P\) に下ろした垂線と \(P\) との交点の全体を, \(A\) の \(P\) への正射影とよぶ. 次の問に答えよ.

1. (1)　平面 \(Q\) が平面 \(P\) と角 \(\theta \ ( 0 \lt \theta \lt \dfrac{\pi}{2} )\) で交わっているとする. すなわち, \(P\) と \(Q\) の交線に垂直な平面で \(P , Q\) を切ってできる \(2\) 直線のなす角が \(\theta\) であるとする. \(Q\) 上の長さ \(1\) の線分の \(P\) への正射影の長さの最大値と最小値を求めよ.

2. (2)　(1) の \(Q\) を考える. \(Q\) 上の \(1\) 辺の長さが \(1\) である正三角形の \(P\) への正射影の面積を求めよ.

3. (3)　\(1\) 辺の長さが \(1\) である正四面体 \(T\) の \(P\) への正射影 \(T'\) はどんな形か. また, \(T'\) の面積の最大値を求めよ.

【 解 答 】

(1)

\(P\) と \(Q\) の交線を \(x\) 軸, \(P\) を \(xy\) 平面となるように空間座標をとる.

\(Q\) 上に \(x\) 軸となす角が \(\phi \ \left( -\dfrac{\pi}{2} \leqq \phi \leqq \dfrac{\pi}{2} \right) \quad ... [1]\) である長さ \(1\) の線分 OX をとると \[ \text{X} \left( \cos \phi , \sin \phi \cos \theta , \sin \phi \sin \theta \right) \] なので, OX の \(P\) への正射影 OX' の長さは \[\begin{align} \text{OX'} & = \sqrt{\cos^2 \phi +( \sin \phi \cos \theta )^2} \\ & = \sqrt{1 -\left( 1 -\cos^2 \theta \right) \sin^2 \phi} \\ & = \sqrt{1 -\sin^2 \phi \sin^2 \theta} \end{align}\] \(0 \leqq \sin^2 \phi \leqq 1\) なので \[ \sqrt{1 -\sin^2 \theta} = \cos \theta \leqq \text{OX'} \leqq 1 \] よって, 最大値は \(\underline{1}\) , 最小値は \(\underline{\cos \theta}\) .

(2)

\(1\) 辺を OX と考えれば, 他の \(1\) 辺 OY は \(x\) 軸と角 \(\phi +\dfrac{\pi}{3}\) をなすと考えられる.
(1) の経過より \[ \text{X} \left( \cos \phi , \sin \left( \phi +\dfrac{\pi}{3} \right) \cos \theta , \sin \left( \phi +\dfrac{\pi}{3} \right) \sin \theta \right) \] よって, 求める面積 \(S\) は \[\begin{align} S & = \dfrac{1}{2} \left| \cos \phi \cdot \sin \left( \phi +\dfrac{\pi}{3} \right) \cos \theta -\cos \phi \cdot \sin \phi \cos \theta \right| \\ & = \dfrac{1}{2} \left| \cos \theta \sin \left\{ \left( \phi +\dfrac{\pi}{3} \right) -\phi \right\} \right| \\ & = \dfrac{1}{2} \cdot \dfrac{\sqrt{3}}{2} \cos \theta \quad ( \ \text{∵} \ [1] \ ) \\ & = \underline{\dfrac{\sqrt{3}}{4} \cos \theta} \end{align}\]

(3)

\(T'\) の面積を \(|T'|\) とおく.
\(T\) の \(4\) つの面のうち \(1\) つを底面 \(B\) , これに含まれない点を頂点 A と表す.
\(B\) , A の正射影をそれぞれ \(B'\) , A'とおくと

1. 1*　A' が \(B'\) の周および内部に含まれるとき, \(T'\) は三角形

2. 2*　A' が \(B'\) の外部にあるとき, \(T'\) は四角形

それぞれの場合について考える.

1. 1*　三角形の場合
   (2) の結果から \[ |T'| = \dfrac{\sqrt{3}}{4} \cos \theta \leqq \dfrac{\sqrt{3}}{4} \] 等号成立は, \(\theta = 0\) のとき, すなわち, \(1\) つの面が \(P\) と平行であるとき.

2. 2*　四角形の場合
   四角形の対角線の長さを \(p , q\) , 対角線どうしのなす角を \(\alpha\) とおくと \[ |T'| = \dfrac{1}{2} pq \sin \alpha \leqq \dfrac{1}{2} \] 等号成立は, \(p = q = 1 , \ \alpha = \dfrac{\pi}{2} \quad ... [2]\) のとき.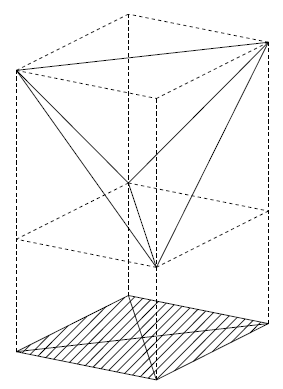 ここで, \(1\) 組の対辺が \(P\) と平行であるときについて考えると, 対辺は垂直であるから, \(\alpha = \dfrac{\pi}{2}\) , (1) の結果より, \(p = q = 1\) なので, [2] の場合をみたしている.

以上より, \(T'\) の形は \(\underline{\text{三角形, 四角形}}\) であり, \(\dfrac{\sqrt{3}}{4} \lt \dfrac{1}{2}\) なので, 面積の最大値は \(\underline{\dfrac{1}{2}}\) .