四面体 OABC において \(\text{OA} = \text{BC} = 2\) , \(\text{OB} = 3\) , \(\text{OC} = \text{AB} = 4\) , \(\text{AC} = 2 \sqrt{6}\) である. また, \(\overrightarrow{a} = \overrightarrow{\text{OA}}\) , \(\overrightarrow{b} = \overrightarrow{\text{OB}}\) , \(\overrightarrow{c} = \overrightarrow{\text{OC}}\) とする. 以下の問に答えよ.
(1) 内積 \(\overrightarrow{a} \cdot \overrightarrow{b}\) , \(\overrightarrow{a} \cdot \overrightarrow{c}\) , \(\overrightarrow{b} \cdot \overrightarrow{c}\) を求めよ.
(2) \(\triangle \text{OAB}\) を含む平面を \(H\) とする. \(H\) 上の点 P で直線 PC と \(H\) が直交するものをとる. このとき, \(\overrightarrow{\text{OP}} = x \overrightarrow{a} +y \overrightarrow{b}\) となる \(x , y\) を求めよ.
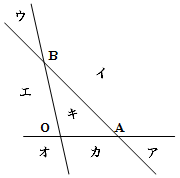
(3) 平面 \(H\) を直線 OA , AB , BO で下図のように \(7\) つの領域ア, イ, ウ, エ, オ, カ, キにわける. 点 P はどの領域に入るか答えよ.
- (4) 辺 AB で △ABC と △OAB のなす角は鋭角になるか, 直角になるか, それとも鈍角になるかを判定せよ. ただし, \(1\) 辺を共有する \(2\) つの三角形のなす角とは, 共有する辺に直交する平面での \(2\) つの三角形の切り口のなす角のことである.
【 解 答 】
(1)
\(\left| \overrightarrow{a} \right| = 2\) , \(\left| \overrightarrow{b} \right| = 3\) , \(\left| \overrightarrow{c} \right| = 4\) を用いて \[\begin{gather} \left| \overrightarrow{a} -\overrightarrow{b} \right|^2 = 4 +9 - 2\overrightarrow{a} \cdot \overrightarrow{b} = 16 \\ \text{∴} \quad \overrightarrow{a} \cdot \overrightarrow{b} = \underline{-\dfrac{3}{2}} , \\ \left| \overrightarrow{c} -\overrightarrow{a} \right|^2 = 16 +4 - 2\overrightarrow{a} \cdot \overrightarrow{c} = 24 \\ \text{∴} \quad \overrightarrow{a} \cdot \overrightarrow{c} = \underline{-2} , \\ \left| \overrightarrow{b} -\overrightarrow{c} \right|^2 = 9 +16 - 2\overrightarrow{a} \cdot \overrightarrow{b} = 4 \\ \text{∴} \quad \overrightarrow{b} \cdot \overrightarrow{c} = \underline{\dfrac{21}{2}} \end{gather}\]
(2)
PC と平面 \(H\) は垂直なので \[ \overrightarrow{\text{CP}} \perp \overrightarrow{\text{OA}} , \ \overrightarrow{\text{CP}} \perp \overrightarrow{\text{OB}} \] したがって, \[\begin{align} \left( x \overrightarrow{a} +y \overrightarrow{b} -\overrightarrow{c} \right) \cdot \overrightarrow{a} & = 4x -\dfrac{3y}{2} +2 = 0 \\ \text{∴} \quad 8x-3y & = -4 \quad ... [1] , \\ \left( x \overrightarrow{a} +y \overrightarrow{b} -\overrightarrow{c} \right) \cdot \overrightarrow{b} & = -\dfrac{3x}{2} +9y -\dfrac{21}{2} = 0 \\ \text{∴} \quad x-6y & = 7 \quad ... [2] \end{align}\] [1] [2] を解けば \[ x = \underline{-\dfrac{1}{15}} , \ y = \underline{\dfrac{52}{45}} \]
(3)
(2) の結果より
\[
\overrightarrow{\text{OH}} =\dfrac{-3 \overrightarrow{a} +52 \overrightarrow{b}}{45} = \dfrac{49}{45} \cdot \dfrac{-3 \overrightarrow{a} +52 \overrightarrow{b}}{49}
\]
なので, 線分 AB を \(52 : 3\) に外分する点を Q とするとき, 点 P は線分 OQ を \(49 : 4\) に外分する点である.
ゆえに, 点 P を含む領域は
\[
\underline{\text{ウ}}
\]
(4)
(3) の結果より, 点 P が直線 AB について, 点 O と反対側にあるので, △ABC と △OAB のなす角は \[ \underline{\text{鈍角}} \]