\(-\dfrac{1}{4} \lt s \lt \dfrac{1}{3}\) とする. \(xyz\) 空間内の平面 \(z = 0\) の上に長方形 \[ R _ s = \left\{ ( x , y , 0 ) | 1 \leqq x \leqq 2+4s , 1 \leqq y \leqq 2-3s \right\} \] がある. 長方形 \(R _ s\) を \(x\) 軸のまわりに \(1\) 回転してできる立体を \(K _ s\) とする.
(1) 立体 \(K _ s\) の体積 \(V(s)\) が最大となるときの \(s\) の値, およびそのときの \(V(s)\) の値を求めよ.
(2) \(s\) を (1) で求めた値とする. このときの立体 \(K _ s\) を \(y\) 軸のまわりに \(1\) 回転してできる立体 \(L\) の体積を求めよ.
【 解 答 】
(1)
\(-\dfrac{1}{4} \lt s \lt \dfrac{1}{3} \quad ... [1]\) のとき, \(R _ s\) は下図斜線部のようになる.
\[\begin{align} V(s) & = \pi \left\{ (2-3s)^2 -1^2 \right\} (1+4s) \\ & = 3 \pi ( 3s^2-4s+1 )( 4s+1 ) \\ & = 3 \pi ( \underline{12s^3-13s+1} ) \end{align}\] 下線部を \(f(s)\) とおくと \[ f'(s) = 36s^2-26s = 2s( 18s-13 ) \] [1] の範囲で \(f'(s)=0\) をとくと \[ s=0 \] したがって, \(f(s)\) の増減表は下のようになり, \[ \begin{array}{c|ccccc} s & -\dfrac{1}{4} & \cdots & 0 & \cdots & \dfrac{1}{3} \\ \hline f'(s) & & + & 0 & 1 & \\ \hline f(s) & & \searrow & \text{最大} & \nearrow & \end{array} \] 最大値は \[ f(0) = 1 \] よって \(V(s)\) は, \(s = \underline{0}\) のとき最大となり, \(V(0) =\underline{3 \pi}\) .
(2)
\(K _ 0\) は \(xz\) 平面について対称なので, \(y \gt 0\) の部分について考える.
\(K _ 0\) を \(x\) 軸方向から見ると右図のようになる.
\(K _ 0\) の平面 \(y = t \ ( 0 \leqq t \leqq 2 )\) による断面図から, \(L\) の断面積を求めていく.
1* \(1 \leqq t \leqq 2\) のとき
\(K _ 0\) の断面は下図のようになる.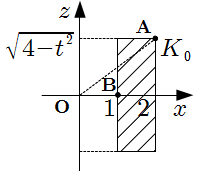
\[\begin{align}
\text{OA} & = \sqrt{(4-t^2)+2^2} = \sqrt{8-t^2} , \\
\text{OB} & = 1
\end{align}\]
したがって, \(L\) の断面積 \(T(t)\) は
\[
T(t)= ( \text{OA}^2-\text{OB}^2 ) \pi = (7-t^2) \pi
\]2* \(0 \leqq t \leqq 1\) のとき
\(K _ 0\) の断面は下図のようになる.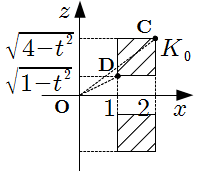
\[\begin{align}
\text{OC} & = \sqrt{(4-t^2)+2^2} = \sqrt{8-t^2} , \\
\text{OD} & = \sqrt{(1-t^2)+1^2} = \sqrt{2-t^2}
\end{align}\]
したがって, \(L\) の断面積 \(T(t)\) は
\[
T(t) = ( \text{OA}^2-\text{OB}^2 ) \pi = 6 \pi
\]
\[\begin{align}
\text{OA} & = \sqrt{(4-t^2)+2^2} = \sqrt{8-t^2} , \\
\text{OB} & = 1
\end{align}\]
したがって, \(L\) の断面積 \(T(t)\) は
\[
T(t)= ( \text{OA}^2-\text{OB}^2 ) \pi = (7-t^2) \pi
\]
\[\begin{align}
\text{OC} & = \sqrt{(4-t^2)+2^2} = \sqrt{8-t^2} , \\
\text{OD} & = \sqrt{(1-t^2)+1^2} = \sqrt{2-t^2}
\end{align}\]
したがって, \(L\) の断面積 \(T(t)\) は
\[
T(t) = ( \text{OA}^2-\text{OB}^2 ) \pi = 6 \pi
\]1* 2* より求める体積 \(W\) は \[\begin{align} W & = 2 \left\{ 6 \pi \cdot 1 +\displaystyle\int _ 1^2 (7-t^2) \pi \, dt \right\} \\ & = 12 \pi +14 \pi - 2\pi \left[ \dfrac{t^3}{3} \right] _ 1^2 \\ & = \left( 26-\dfrac{14}{3} \right) \pi =\underline{\dfrac{64 \pi}{3}} \end{align}\]