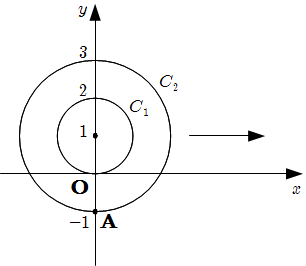
半径 \(1\) の円盤 \(C_1\) が半径 \(2\) の円盤 \(C_2\) に貼り付けられており, \(2\) つの円盤の中心は一致する. \(C_2\) の周上にある定点を A とする. 図のように, 時刻 \(t=0\) において \(C_1\) はO \((0,0)\) で \(x\) 軸に接し, A は座標 \((0,-1)\) の位置にある. \(2\) つの円盤は一体となり, \(C_1\) は \(x\) 軸上をすべることなく転がっていく. 時刻 \(t\) で \(C_1\) の中心が \((t,1)\) にあるように転がるとき, \(0 \leqq t \leqq 2 \pi\) において A が描く曲線を \(C\) とする.
(1) 時刻 \(t\) における A の座標を \(\left( x(t) , y(t) \right)\) で表す. \(\left( x(t) , y(t) \right)\) を求めよ.
(2) \(x(t)\) と \(y(t)\) の \(t\) に関する増減を調べ, \(x(t)\) あるいは \(y(t)\) が最大値または最小値をとるときの A の座標を全て求めよ.
(3) \(C\) と \(x\) 軸で囲まれた図形の面積を求めよ.
【 解 答 】
(1)
時刻 \(t\) における \(C_1 , C_2\) の中心を P, \(C_1\) と \(x\) 軸の接点を T とおくと \[ \text{P} ( t , 1 ) , \ \text{T} ( t , 0 ) , \ \angle\text{TPA} = t \ . \] なので, 求める A の座標は \[ \left( x(t) , y(t) \right) = \underline{\left( t -2 \sin t , 1 -2\cos t \right)} \ . \]
(2)
(1) の結果より \[ \begin{align} x'(t) & = 1 -2\cos t \ , \\ y'(t) & = 2 \sin t \ . \end{align} \] \(x'(t) = 0\) をとくと \[ t = \dfrac{\pi}{3} , \dfrac{5 \pi}{3} \ . \] \(y'(t) = 0\) をとくと \[ t = 0 , \pi , 2 \pi \ . \] したがって, \(x , y\) の増減は下表のようになる. \[ \begin{array}{c|ccccccccc} t & 0 & \cdots & \frac{\pi}{3} & \cdots & \pi & \cdots & \frac{5 \pi}{3} & \cdots & 2 \pi\\ \hline x'(t) & & - & 0 & + & & + & 0 & - & \\ \hline y'(t) & 0 & + & & + & 0 & - & & - & 0 \\ \hline x(t) & 0 & \leftarrow & \frac{\pi}{3} -\sqrt{3} & \rightarrow & \pi & \rightarrow & \frac{5 \pi}{3} +\sqrt{3} & \leftarrow & 2 \pi \\ \hline y(t) & -1 & \uparrow & 0 & \uparrow & 3 & \downarrow & 0 & \downarrow & -1 \end{array} \\ \] 以上より, 求める A の座標は
\(x(t)\) が最小になるとき, \(\underline{\left( \dfrac{\pi}{3} -\sqrt{3} , 0 \right)}\)
\(x(t)\) が最大になるとき, \(\underline{\left( \dfrac{5 \pi}{3} +\sqrt{3} , 0 \right)}\)
\(y(t)\) が最小になるとき, \(\underline{( 0 , -1 ) , \ ( 2 \pi , -1 )}\)
\(y(t)\) が最大になるとき, \(\underline{( \pi , 3 )}\)
(3)
(2) の結果より, \(C\) と \(x\) 軸に囲まれた図形は下図のようになる.
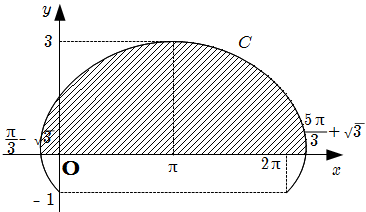
よって, 求める面積 \(S\) は \[\begin{align} S & = \displaystyle\int_{\frac{\pi}{3} -\sqrt{3}}^{\frac{5 \pi}{3} +\sqrt{3}} y(t) \, dx \\ & = \displaystyle\int_{\frac{\pi}{3}}^{\frac{5 \pi}{3}} y(t) x'(t) \, dt \\ & = \displaystyle\int_{\frac{\pi}{3}}^{\frac{5 \pi}{3}} \left( 1 -2 \cos t \right)^2 \, dt \\ & = \displaystyle\int_{\frac{\pi}{3}}^{\frac{5 \pi}{3}} \left( 1 -4 \cos t +4 \cdot \dfrac{1 +\cos 2t}{2}\right) \, dt \\ & = \left[ 3t -4 \sin t +\sin 2t \right]_{\frac{\pi}{3}}^{\frac{5 \pi}{3}} \\ & = \underline{4 \pi +3 \sqrt{3}} \ . \end{align}\]