\(p , q\) を実数とする. 放物線 \(y = x^2-2px+q\) が, 中心 \((p, 2p)\) で半径 \(1\) の円と中心 \((p, p)\) で半径 \(1\) の円の両方と共有点をもつ. この放物線の頂点が存在しうる領域を \(xy\) 平面上に図示せよ.

【 解 答 】

放物線の頂点を \(( X, Y )\) とおく. \[ y = x^2 -2px +q = (x-p)^2-p^2+q \] なので \[\begin{align} X = p & , \ Y = -p^2+q \\ \text{∴} \quad p = X & , \ q = X^2+Y \quad ... [1] \end{align}\] 放物線の頂点, 円の中心がすべて \(x=p\) 上にあることから, \(y = x^2\) と \(y\) 軸に中心をもつ半径 \(1\) の円が共有点をもつための放物線の頂点と, 円の中心の距離 \(h\) についての条件を考えればよい.

1. 1*　円が放物線より下側にあるとき
   明らかに, \(h \leqq 1\) .

2. 2*　円が放物線より上側にあるとき 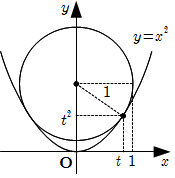\(h\) が最大となるのは上図のように, 円と放物線が \(x\) 座標が \(t \ ( 0 \lt t \lt 1 )\) の点で接するときである.
   \(y' = 2x\) より, この点での法線の傾きは \(-\dfrac{1}{2t}\) なので \[\begin{align} t^2 & +\left( \dfrac{1}{2} \right)^2 = 1^2 \\ \text{∴} \quad t & = \dfrac{\sqrt{3}}{2} \end{align}\] したがって \[ h \leqq \left( \dfrac{\sqrt{3}}{2} \right)^2 +\dfrac{1}{2} = \dfrac{5}{4} \]

1* 2* より, 求める条件は [1] も用いれば \[\begin{align} & \left\{ \begin{array}{l} Y-1 \leqq X \leqq Y+\dfrac{5}{4} \\ Y-1 \leqq 2 (X^2+Y) \leqq Y+\dfrac{5}{4} \end{array} \right. \\ \text{∴} \quad & \left\{ \begin{array}{l} X-\dfrac{5}{4} \leqq Y \leqq X+1 \\ -2X^2-1 \leqq Y \leqq -2X^2+\dfrac{5}{4} \end{array} \right. \end{align}\] この領域を図示すれば下図斜線部（境界を含む）.