\(2\) 次以下の整式 \(f(x) = ax^2+bx+c\) に対し \[ S = \displaystyle\int _ 0^2 \left| f'(x) \right| \, dx \] を考える.
(1) \(f(0) = 0\) , \(f(2) = 2\) のとき \(S\) を \(a\) の関数として表せ.
(2) \(f(0) = 0\) , \(f(2) = 2\) をみたしながら \(f\) が変化するとき, \(S\) の最小値を求めよ.
【 解 答 】
(1)
条件より \[\begin{align} f(0) & = c = 0 , \\ f(2) & = 4a+2b+c = 2 \\ \text{∴} \quad b & = 1-2a , \ c = 0 \end{align}\] したがって, \(f(x) = ax^2 +(1-2a) x\) なので \[ f'(x) = 2ax -2a+1 \] \(f'(1) = 1\) で傾き \(2a\) の直線であることから, 場合分けして考える.
1* \(a \leqq -\dfrac{1}{2}\) のとき
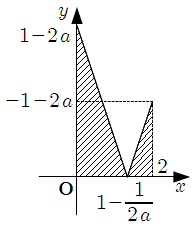 \[\begin{align}
S & = \dfrac{1}{2} ( 1-2a ) \left( 1 -\dfrac{1}{2a} \right) +\dfrac{1}{2} ( -1-2a ) \left( 1 +\dfrac{1}{2a} \right) \\
& = -\dfrac{(1-2a)^2}{4a} -\dfrac{(1+2a)^2}{4a} \\
& = -2a -\dfrac{1}{2a}
\end{align}\]
\[\begin{align}
S & = \dfrac{1}{2} ( 1-2a ) \left( 1 -\dfrac{1}{2a} \right) +\dfrac{1}{2} ( -1-2a ) \left( 1 +\dfrac{1}{2a} \right) \\
& = -\dfrac{(1-2a)^2}{4a} -\dfrac{(1+2a)^2}{4a} \\
& = -2a -\dfrac{1}{2a}
\end{align}\]2* \(\dfrac{1}{2} \lt a \lt -\dfrac{1}{2}\) のとき
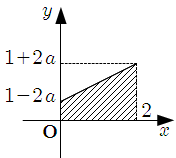 \[\begin{align}
S & = \dfrac{1}{2} \left\{ (1+2a) +(1-2a) \right\} \cdot 2 \\
& = 2
\end{align}\]
\[\begin{align}
S & = \dfrac{1}{2} \left\{ (1+2a) +(1-2a) \right\} \cdot 2 \\
& = 2
\end{align}\]3* \(a \geqq \dfrac{1}{2}\) のとき
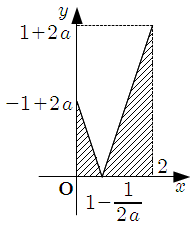 \[\begin{align}
S & = \dfrac{1}{2} ( -1+2a ) \left( 1 -\dfrac{1}{2a} \right) +\dfrac{1}{2} ( 1+2a ) \left( 1 +\dfrac{1}{2a} \right) \\
& = \dfrac{(1-2a)^2}{4a} +\dfrac{(1+2a)^2}{4a} \\
& = 2a +\dfrac{1}{2a}
\end{align}\]
\[\begin{align}
S & = \dfrac{1}{2} ( -1+2a ) \left( 1 -\dfrac{1}{2a} \right) +\dfrac{1}{2} ( 1+2a ) \left( 1 +\dfrac{1}{2a} \right) \\
& = \dfrac{(1-2a)^2}{4a} +\dfrac{(1+2a)^2}{4a} \\
& = 2a +\dfrac{1}{2a}
\end{align}\]
よって, 1*~3*より \[ S = \underline{\left\{ \begin{array}{ll} -2a -\dfrac{1}{2a} & \left( \ a \leqq -\dfrac{1}{2} \text{のとき} \right) \\ 2 & \left( \ -\dfrac{1}{2} \lt a \lt \dfrac{1}{2} \text{のとき} \right) \\ 2a +\dfrac{1}{2a} & \left( \ a \geqq \dfrac{1}{2} \text{のとき} \right) \end{array} \right.} \]
(2)
(1) の結果より, \(|a| \geqq \dfrac{1}{2}\) のとき, 相加相乗平均の関係を用いて \[\begin{align} S & = |2a| +\dfrac{1}{|2a|} \\ & \geqq 2 \sqrt{|2a| \cdot \dfrac{1}{|2a|}} = 2 \end{align}\] 等号が成立するのは \[\begin{align} |2a| & = \dfrac{1}{|2a|} \\ \text{∴} \quad a & = \pm \dfrac{1}{2} \end{align}\] よって, \(S\) は \(|a| \leqq \dfrac{1}{2}\) のとき, 最小値 \(\underline{2}\) をとる.
 \[\begin{align}
S & = \dfrac{1}{2} ( 1-2a ) \left( 1 -\dfrac{1}{2a} \right) +\dfrac{1}{2} ( -1-2a ) \left( 1 +\dfrac{1}{2a} \right) \\
& = -\dfrac{(1-2a)^2}{4a} -\dfrac{(1+2a)^2}{4a} \\
& = -2a -\dfrac{1}{2a}
\end{align}\]
\[\begin{align}
S & = \dfrac{1}{2} ( 1-2a ) \left( 1 -\dfrac{1}{2a} \right) +\dfrac{1}{2} ( -1-2a ) \left( 1 +\dfrac{1}{2a} \right) \\
& = -\dfrac{(1-2a)^2}{4a} -\dfrac{(1+2a)^2}{4a} \\
& = -2a -\dfrac{1}{2a}
\end{align}\] \[\begin{align}
S & = \dfrac{1}{2} \left\{ (1+2a) +(1-2a) \right\} \cdot 2 \\
& = 2
\end{align}\]
\[\begin{align}
S & = \dfrac{1}{2} \left\{ (1+2a) +(1-2a) \right\} \cdot 2 \\
& = 2
\end{align}\] \[\begin{align}
S & = \dfrac{1}{2} ( -1+2a ) \left( 1 -\dfrac{1}{2a} \right) +\dfrac{1}{2} ( 1+2a ) \left( 1 +\dfrac{1}{2a} \right) \\
& = \dfrac{(1-2a)^2}{4a} +\dfrac{(1+2a)^2}{4a} \\
& = 2a +\dfrac{1}{2a}
\end{align}\]
\[\begin{align}
S & = \dfrac{1}{2} ( -1+2a ) \left( 1 -\dfrac{1}{2a} \right) +\dfrac{1}{2} ( 1+2a ) \left( 1 +\dfrac{1}{2a} \right) \\
& = \dfrac{(1-2a)^2}{4a} +\dfrac{(1+2a)^2}{4a} \\
& = 2a +\dfrac{1}{2a}
\end{align}\]