図のように, 正三角形を \(9\) つの部屋に辺で区切り, 部屋 P , Q を定める. \(1\) つの球が部屋 P を出発し, \(1\) 秒ごとに, そのままその部屋にとどまることなく, 辺を共有する隣の部屋に等確率で移動する. 球が \(n\) 秒後に部屋 Q にある確率を求めよ.

【 解 答 】
下図のように部屋 R をおく.

球の動き方から, 球は, 奇数秒後には上図斜線部の部屋のいずれかにあり, 偶数秒後には部屋 P , Q , R のいずれかにある.
\(n\) 秒後に部屋 P , Q , R に球がある確率を \(p _ n , q _ n , r _ n\) とおく.
1* \(n\) が奇数のとき \[ p _ n =q _ n =r _ n = 0 \]
2* \(n\) が偶数のとき \[ p _ n +q _ n +r _ n = 1 \quad ... [1] \] \(n\) 秒後から \(n+2\) 秒後への状態遷移は下図のようになる.
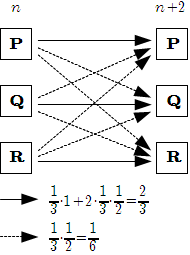 [1] を用いて, \(r _ n\) を消去すると
\[\begin{align}
q _ {n+2} & = \dfrac{1}{6} p _ n +\dfrac{2}{3} q _ n +\dfrac{1}{6} r _ n \\
& = \dfrac{1}{6} +\dfrac{1}{2} q _ n \quad ... [2]
\end{align}\]
[2] より
\[
q _ {n+2} -\dfrac{1}{3} = \dfrac{1}{2} \left( q _ n -\dfrac{1}{3} \right)
\]
\(q _ 0 = 0\) なので
\[\begin{align}
q _ n -\dfrac{1}{3} & = \dfrac{1}{2^{\frac{n}{2}}} \left( 0 -\dfrac{1}{3} \right) \\
\text{∴} \quad q _ n & = \dfrac{1}{3} \left( 1 -\dfrac{1}{2^{\frac{n}{2}}} \right)
\end{align}\]
[1] を用いて, \(r _ n\) を消去すると
\[\begin{align}
q _ {n+2} & = \dfrac{1}{6} p _ n +\dfrac{2}{3} q _ n +\dfrac{1}{6} r _ n \\
& = \dfrac{1}{6} +\dfrac{1}{2} q _ n \quad ... [2]
\end{align}\]
[2] より
\[
q _ {n+2} -\dfrac{1}{3} = \dfrac{1}{2} \left( q _ n -\dfrac{1}{3} \right)
\]
\(q _ 0 = 0\) なので
\[\begin{align}
q _ n -\dfrac{1}{3} & = \dfrac{1}{2^{\frac{n}{2}}} \left( 0 -\dfrac{1}{3} \right) \\
\text{∴} \quad q _ n & = \dfrac{1}{3} \left( 1 -\dfrac{1}{2^{\frac{n}{2}}} \right)
\end{align}\]
以上より, 求める確率は \[ \underline{\left\{ \begin{array}{ll} 0 & ( \ n \text{が奇数のとき} ) \\ \dfrac{1}{3} \left( 1 -\dfrac{1}{2^{\frac{n}{2}}} \right) & ( \ n \text{が偶数のとき} ) \end{array} \right.} \]
 [1] を用いて, \(r _ n\) を消去すると
\[\begin{align}
q _ {n+2} & = \dfrac{1}{6} p _ n +\dfrac{2}{3} q _ n +\dfrac{1}{6} r _ n \\
& = \dfrac{1}{6} +\dfrac{1}{2} q _ n \quad ... [2]
\end{align}\]
[2] より
\[
q _ {n+2} -\dfrac{1}{3} = \dfrac{1}{2} \left( q _ n -\dfrac{1}{3} \right)
\]
\(q _ 0 = 0\) なので
\[\begin{align}
q _ n -\dfrac{1}{3} & = \dfrac{1}{2^{\frac{n}{2}}} \left( 0 -\dfrac{1}{3} \right) \\
\text{∴} \quad q _ n & = \dfrac{1}{3} \left( 1 -\dfrac{1}{2^{\frac{n}{2}}} \right)
\end{align}\]
[1] を用いて, \(r _ n\) を消去すると
\[\begin{align}
q _ {n+2} & = \dfrac{1}{6} p _ n +\dfrac{2}{3} q _ n +\dfrac{1}{6} r _ n \\
& = \dfrac{1}{6} +\dfrac{1}{2} q _ n \quad ... [2]
\end{align}\]
[2] より
\[
q _ {n+2} -\dfrac{1}{3} = \dfrac{1}{2} \left( q _ n -\dfrac{1}{3} \right)
\]
\(q _ 0 = 0\) なので
\[\begin{align}
q _ n -\dfrac{1}{3} & = \dfrac{1}{2^{\frac{n}{2}}} \left( 0 -\dfrac{1}{3} \right) \\
\text{∴} \quad q _ n & = \dfrac{1}{3} \left( 1 -\dfrac{1}{2^{\frac{n}{2}}} \right)
\end{align}\]