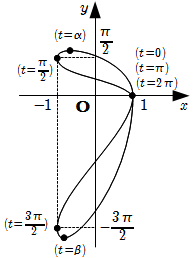解答はこちら »

【 解 答 】

(1)

\(f\) に対応する \(2\) 次正方行列を \(A\) とおくと \[ A = \left( \begin{array}{cc} 3 & 1 \\ -2 & 0 \end{array} \right) \] \(l _ n : \ a _ n x +b _ n y =1\) 上の \(2\) 点 \(\left( \dfrac{1}{a _ n} , 0 \right) , \left( 0 , \dfrac{1}{b _ n} \right)\) は, \(f\) によって \[\begin{align} \left( \begin{array}{cc} 3 & 1 \\ -2 & 0 \end{array} \right) \left( \begin{array}{c} \dfrac{1}{a _ n} \\ 0 \end{array} \right) & = \left( \begin{array}{c} \dfrac{3}{a _ n} \\ -\dfrac{2}{a _ n} \end{array} \right) \\ \left( \begin{array}{cc} 3 & 1 \\ -2 & 0 \end{array} \right) \left( \begin{array}{c} 0 \\ \dfrac{1}{b _ n} \end{array} \right) & = \left( \begin{array}{c} \dfrac{1}{b _ n} \\ 0 \end{array} \right) \end{align}\] の \(2\) 点に移るので, \(l _ {n+1}\) の式は \[\begin{align} \left( \dfrac{3}{a _ n} -\dfrac{1}{b _ n} \right) y -\left( -\dfrac{2}{a _ n} -0 \right) x & = 0 \\ 2 b _ n x +( -a _ n +3 b _ n ) y & = 2 \\ \text{∴} \quad b _ n x +\dfrac{-a _ n +3 b _ n}{2} y & = 1 \end{align}\] よって \[ a _ {n+1} =\underline{b _ n} , \quad b _ {n+1} =\underline{\dfrac{-a _ n +3 b _ n}{2}} \]

(2)

(1) の結果より \[\begin{align} 2 a _ {n+2} -3 a _ {n+1} +a _ n & = 0 \\ \text{∴} \quad 2 a _ {n+2} -a _ {n+1} & = 2 a _ {n+1} -a _ n \end{align}\] これを繰り返し用いれば \[\begin{align} 2 a _ {n+1} -a _ n = 2 b _ 1 -a _ 1 & = 2 \cdot 2 -3 = 1 \\ \text{∴} \quad a _ {n+1} -1 & = \dfrac{1}{2} ( a _ n -1 ) \end{align}\] したがって, 数列 \(\left\{ a _ n -1 \right\}\) は, 公比 \(\dfrac{1}{2}\) , 初項 \(a _ 1 -1 =3-1 =2\) の等比数列なので \[\begin{align} a _ n -1 & = \left( \dfrac{1}{2} \right)^{n-1} \cdot 2 = 2^{2-n} \\ \text{∴} \quad a _ n & = 2^{2-n} +1 \end{align}\] 再び (1) の結果を用いて \[ b _ n = a _ {n+1} = 2^{1-n} +1 \] \(l _ n\) の \(x\) 切片 \(\dfrac{1}{a _ n}\) , \(y\) 切片 \(\dfrac{1}{b _ n}\) に着目すると, \(n \geqq 0\) に対して \[\begin{align} \dfrac{1}{3} \leqq \dfrac{1}{a _ n} & = \dfrac{1}{2^{2-n} +1} \lt 1 \\ \dfrac{1}{2} \leqq \dfrac{1}{b _ n} & = \dfrac{1}{2^{1-n} +1} \lt 1 \end{align}\] また, \(l _ n\) が \(n\) によらず通る点について考えると \[\begin{align} ( 2^{2-n}+1 )x +( 2^{1-n}+1 )y & =1 \\ (2x+y) 2^{1-n} +x+y-1 & = 0 \end{align}\] なので \[\begin{align} \left\{ \begin{array}{l} 2x+y=0 \\ x+y-1 =0 \end{array} \right. \\ \text{∴} \quad (x,y) = ( -1 , 2 ) \end{align}\] 以上より, 求める領域はすべての \(l _ n\) （ \(n =0, 1, 2, \cdots\) ）に対して上側となる領域で, 下図の斜線部（実線は含み, 破線と○は含まない）.

« 解答を隠す

解答はこちら »

【 解 答 】

(1)

操作 (A) を \(n\) 回繰り返した後, \(2\) 色のカードが \(2\) 枚ずつとなる確率を \(a _ n\) , \(1\) 枚と \(3\) 枚である確率を \(b _ n\) とおく. ただし, \(1\) 度でも \(4\) 枚のカードが同じ色になる場合は除いて考える.
このとき \[\begin{align} a _ {n+1} =\dfrac{3}{4} b _ n & , \quad b _ {n+1} =a _ n \\ \text{∴} \quad b _ {n+2} & = \dfrac{3}{4} b _ n \end{align}\] \(b _ 0 =0\) , \(b _ 1 =1\) なので

• \(n\) が偶数のとき　\(b _ n =0\)

• \(n\) が奇数のとき　\(b _ n =\left( \dfrac{3}{4} \right)^{\frac{n-1}{2}}\)

求める確率は, \(\dfrac{1}{4} b _ {n-1} \quad ( n \geqq 2 )\) と表せるので

• \(n\) が偶数のとき　\(\underline{\dfrac{1}{4} \left( \dfrac{3}{4} \right)^{\frac{n}{2}-1}}\)

• \(n\) が奇数のとき　\(\underline{0}\)

(2)

操作 (A) を \(n\) 回繰り返した後, \(2\) 色のカードが \(3\) 枚ずつとなる確率を \(p _ n\) , \(2\) 枚と \(4\) 枚である確率を \(q _ n\) , \(1\) 枚と \(5\) 枚である確率を \(r _ n\) とおく. ただし, \(1\) 度でも \(6\) 枚のカードが同じ色になる場合は除いて考える.
このとき \[\begin{align} p _ {n+1} & = \dfrac{2}{3} q _ n , \quad q _ {n+1} =p _ n +\dfrac{5}{6} r _ n , \quad r _ {n+1} =\dfrac{1}{3} q _ n \\ \text{∴} \quad q _ {n+2} & =p _ {n+1} +\dfrac{5}{6} r _ {n+1} = \dfrac{2}{3} q _ n +\dfrac{5}{18} q _ n = \dfrac{17}{18} q _ n \end{align}\] \(q _ 0 =0\) , \(q _ 1 =1\) なので,

• \(n\) が偶数のとき　\(q _ n =0\)

• \(n\) が奇数のとき　\(q _ n =\left( \dfrac{17}{18} \right)^{\frac{n-1}{2}}\)

求める確率は, \(\dfrac{1}{3} \cdot \dfrac{1}{6} q _ {n-2} =\dfrac{1}{18} q _ {n-2}\) （ \(n \geqq 3\) ）と表せるので

• \(n=1\) , \(n\) が偶数のとき　\(\underline{0}\)

• \(n\) が \(3\) 以上の奇数のとき　\(\underline{\dfrac{1}{18} \left( \dfrac{17}{18} \right)^{\frac{n-3}{2}}}\)

« 解答を隠す

解答はこちら »

【 解 答 】

(1)

(2)

\(h\) を正の実数として, \(\text{G} _ 1 , \text{G} _ 2\) が \(z\) 軸上になるように, 正八面体の \(6\) つの頂点を \[\begin{align} \text{A} \left( \dfrac{\sqrt{3}}{3} , 0 , h \right) , & \quad \text{B} \left( -\dfrac{\sqrt{3}}{6} , \dfrac{1}{2} , h \right) , \quad \text{C} \left( -\dfrac{\sqrt{3}}{6} , -\dfrac{1}{2} , h \right) , \\ \text{D} \left( -\dfrac{\sqrt{3}}{3} , 0 , -h \right) , & \quad \text{E} \left( \dfrac{\sqrt{3}}{6} , \dfrac{1}{2} , -h \right) , \quad \text{F} \left( \dfrac{\sqrt{3}}{6} , -\dfrac{1}{2} , -h \right) \end{align}\] とおく. \(\text{AE} =1\) なので \[\begin{align} \left( \dfrac{\sqrt{3}}{6} \right)^2 + & \left( \dfrac{1}{2} \right)^2 +(2h)^2 =1 \\ 4h^2 & =\dfrac{2}{3} \\ \text{∴} \quad h & =\dfrac{\sqrt{6}}{6} \end{align}\] 対称性から \(z \geqq 0\) の領域について考えればよい.
平面 \(z = t \quad ( 0 \leqq t \leqq h )\) と AE の交点を P とおけば, P は AE を \((h-t) : (h+t)\) に内分する点である.
また, AE の中点を M とおいて, 平面 \(z=t\) での正八面体の切り口を \(z\) 軸方向から見ると, 下図斜線部のようになる.

\[\begin{align} \text{AE} & = \dfrac{\sqrt{3}}{3} , \quad \text{OM} =\dfrac{1}{2} , \\ \text{PM} & = \dfrac{t}{2h} \text{AE} = \dfrac{\sqrt{2} t}{2} \end{align}\] したがって \[ \text{OP}^2 =\left( \dfrac{1}{2} \right)^2 +\left( \dfrac{\sqrt{2} t}{2} \right)^2 =\dfrac{2 t^2+1}{4} \] この図形を \(z\) 軸を中心に回転させてできる円の面積 \(S(t)\) とすると \[ S(t) =\pi \text{OP}^2 =\dfrac{\pi ( 2t^2+1 )}{4} \] よって, 求める体積 \(V\) は \[\begin{align} V & = 2 \displaystyle\int _ 0^{\frac{\sqrt{6}}{6}} S(t) dt \\ & = \dfrac{\pi}{2} \displaystyle\int _ 0^{\frac{\sqrt{6}}{6}} \, (2t^2+1) dt \\ & = \dfrac{\pi}{2} \left[ \dfrac{2t^3}{3} +t \right] _ 0^{\frac{\sqrt{6}}{6}} \\ & =\dfrac{\pi}{2} \left( \dfrac{\sqrt{6}}{54} +\dfrac{\sqrt{6}}{6} \right) \\ & = \underline{\dfrac{5 \sqrt{6} \pi}{54}} \end{align}\]

« 解答を隠す

解答はこちら »

【 解 答 】

(1)

P , Q の \(x\) 座標を \(p , q\) とおくと \[\begin{align} m & = \dfrac{p^2-q^2}{p-q} = p+q , \\ L & = \sqrt{(p-q)^2 +(p^2-q^2)^2} \\ & = \sqrt{(p-q)^2 \left\{ (p+q)^2+1 \right\}} \\ & = \sqrt{\left\{ m^2 -4pq \right\} (m^2+1)} \\ \text{∴} \quad & pq =\dfrac{1}{4} \left( m^2 -\dfrac{L^2}{m^2+1} \right) \end{align}\] したがって \[\begin{align} h & = \dfrac{p^2+q^2}{2} \\ & = \dfrac{1}{2} \left\{ m^2 -\dfrac{1}{2} \left( m^2 -\dfrac{L^2}{m^2+1} \right) \right\} \\ & = \underline{\dfrac{1}{4} \left( m^2 +\dfrac{L^2}{m^2+1} \right)} \end{align}\]

(2)

\(t =m^2+1\) とおくと, \(t \geqq 1\) . \[ h =\dfrac{1}{4} \left(t+\dfrac{L^2}{t} -1 \right) \] \(f(t) =h\) とおくと

1. 1*　\(L \geqq 1\) のとき
   相加相乗平均の関係より \[\begin{align} f(t) & = \dfrac{1}{4} \left( 2 \sqrt{t \cdot \dfrac{L^2}{t}} -1 \right) \\ & = \dfrac{2L-1}{4} \end{align}\] 等号成立は, \(t =\dfrac{L^2}{t}\) すなわち \(t =L\) のとき

2. 2*　\(0 \lt L \lt 1\) のとき \[ f'(t) =\dfrac{1}{4} \left( 1 -\dfrac{L^2}{t^2} \right) \geqq 0 \] したがって, \(f(t)\) は単調増加し \[ f(t) \geqq f(1) =\dfrac{L^2}{4} \] 以上より, 求める最小値は \[ \underline{\left\{ \begin{array}{ll} \dfrac{L^2}{4} & \ \left( \ 0 \lt L \lt 1 \text{のとき} \right) \\ \dfrac{2L-1}{4} & \ \left( \ L \geqq 1 \text{のとき} \right) \end{array} \right.} \]

« 解答を隠す

解答はこちら »

【 解 答 】

(1)

\(f(n) =\dfrac{10^n -1}{9}\) とおく.

1. [A]：『 \(f(3^m)\) は \(3^m\) で割り切れるが, \(3^{m+1}\) では割り切れない』

[A] が \(0\) 以上の整数 \(m\) について成立することを, 数学的帰納法で示す.

1. 1*　\(m=0\) のとき \[ f(3^0) =f(1) =1 \] これは, \(3^0 =1\) で割り切れるが, \(3^1 =3\) では割り切れない.
   したがって, \(m=0\) のとき, [A] は成立する.

2. 2*　\(m=k \ ( k \geqq 0 )\) のとき, [A] が成立すると仮定すると \[\begin{align} f( 3^{k+1}) & = \dfrac{10^{3 \cdot 3^k} -1}{9} \\ & = \dfrac{\left( 10^{3^k} -1 \right) \left( 10^{2 \cdot 3^k} +10^{3^k} +1 \right)}{9} \\ & = f( 3^k ) \underline{\left( 10^{2 \cdot 3^k} +10^{3^k} +1 \right)} _ {[1]} \end{align}\] 下線部 [1] について, \(\mod 3\) とすると \[ [1] \equiv 1^{2 \cdot 3^k} +1^{3^k} +1 \equiv 0 \] \(\mod 9\) とすると \[ [1] \equiv 1^{2 \cdot 3^k} +1^{3^k} +1 \equiv 3 \] なので, [1] は \(3\) で割り切れるが, \(9\) では割り切れない.
   仮定より, \(f(3^k)\) は, \(3^k\) では割り切れるが, \(3^{k+1}\) では割り切れないので, \(f(3^{k+1})\) は, \(3^{k+1}\) では割り切れるが, \(3^{k+2}\) では割り切れない.
   したがって, \(m=k+1\) のときも [A] が成立する.

以上より, 題意は示された.

(2)

1. [P]：『 \(n\) が \(27\) で割り切れる』

2. [Q]：『 \(f(n)\) が \(27\) で割り切れる』

3. 1*　\(\text{[P]} \Longrightarrow \text{[Q]}\) の証明
   \(n =27 i\) （ \(i\) は \(0\) 以上の整数）とおくと \[\begin{align} f(27i) & = \dfrac{10^{27i}-1}{9} \\ & = \dfrac{10^{27}-1}{9} \left\{ 10^{27(i-1)} +10^{27(i-2)} +\cdots +1 \right\} \\ & = f( 3^3 ) \left\{ 10^{27(i-1)} +10^{27(i-2)} +\cdots +1 \right\} \end{align}\] (1) の結果より, \(f(3^3)\) は \(3^3 =27\) で割り切れるので, \(f(27i)\) は27で割り切れる.

4. 2* \(\text{[Q]} \Longrightarrow \text{[P]}\) の証明
   \(f(n)\) は \(1\) が \(n\) 個並んだ数なので,
   \(f(n) =27j\) （ \(j\) は \(0\) 以上の整数）ならば, \(n =27j\) .

以上より, 題意は示された.

« 解答を隠す

解答はこちら »

【 解 答 】

\[\begin{align} \dfrac{dx}{dt} & = -2\sin 2t , \\ \dfrac{dy}{dt} & = \sin t +t \cos t \end{align}\] \(0 \leqq t \leqq 2 \pi\) において \[\begin{align} \dfrac{dx}{dt} & = -2\sin 2t =0 \\ \text{∴} \quad t =0 , & \dfrac{\pi}{2} , \pi , \dfrac{3 \pi}{2} , 2 \pi \end{align}\] また \[\begin{align} \dfrac{dy}{dt} = \sin t +t \cos t & =0 \\ \text{∴} \quad \tan t & = -t \quad ... [1] \end{align}\] \(y= \tan t\) と \(y =-t\) のグラフは下図のようになる.

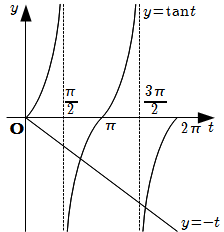
したがって, [1] の解は \[ t = 0 , \alpha , \beta \quad \left( \ \dfrac{\pi}{2} \lt \alpha \lt \pi , \dfrac{3 \pi}{2} \lt \beta <2 \pi \ \right) \] 以上より, \((x, y)\) の増減表は下表の通りとなる. \[ \begin{array}{c|ccccccccccccc} t & 0 & \cdots & \dfrac{\pi}{2} & \cdots & \alpha & \cdots & \pi & \cdots & \dfrac{3 \pi}{2} & \cdots & \beta & \cdots & 2\pi \\ \hline \frac{dx}{dt} & 0 & - & 0 & + & & + & 0 & - & 0 & + & & + & 0 \\ \hline \frac{dy}{dt} & 0 & + & & + & 0 & - & & - & & - & 0 & + & \\ \hline x & 1 & \leftarrow & -1 & \rightarrow & & \rightarrow & 1 & \leftarrow & -1 & \rightarrow & & \rightarrow & 1 \\ \hline y & 0 & \uparrow & \dfrac{\pi}{2} & \uparrow & \max & \downarrow & 0 & \downarrow & -\dfrac{3 \pi}{2} & \downarrow & \min & \uparrow & 0 \end{array} \] ゆえに, 与えられた曲線の概形は下図のようになる.

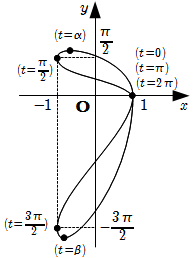
したがって, 求める面積 \(S\) は \[\begin{align} S & = \displaystyle\int _ {t=\frac{\pi}{2}}^{t=\pi} y \, dx -\displaystyle\int _ {t=\frac{\pi}{2}}^{t=0} y \, dx +\displaystyle\int _ {t=\frac{3 \pi}{2}}^{t= 2\pi} (-y) \, dx -\displaystyle\int _ {t=\frac{3 \pi}{2}}^{t=\pi} (-y) \, dx \\ & = \displaystyle\int _ {t=0}^{t=\pi} y \, dx +\displaystyle\int _ {t=2 \pi}^{t=\pi} y \, dx \end{align}\] ここで, \(F(t) =\displaystyle\int y \, dx\) とおくと \[\begin{align} F(t) & =\displaystyle\int \, t \sin t ( -2 \sin 2t ) \, dt \\ & = -4 \displaystyle\int \, t \sin^2 t ( \sin t )' \, dt \\ & = -\dfrac{4}{3} t \sin^3 t +\dfrac{4}{3} \displaystyle\int \, \sin^3 t \, dt \\ & = -\dfrac{4}{3} t \sin^3 t -\dfrac{4}{3} \displaystyle\int \, \left( 1 -\cos^2 t \right) \left( \cos t \right)' \, dt \\ & = -\dfrac{4}{3} t \sin^3 t -\dfrac{4}{3} \left( \cos t -\dfrac{1}{3} \cos^3 t \right) \\ & = -\dfrac{4}{3} t \sin^3 t -\dfrac{4}{3} \cos t +\dfrac{4}{9} \cos^3 t +C \quad ( \ C \text{は積分定数} ) \end{align}\] よって \[\begin{align} S & = 2F( \pi ) -F(0) -F( 2\pi ) \\ & = 2 \left( \dfrac{4}{3} -\dfrac{4}{9} \right) -\left( -\dfrac{4}{3} +\dfrac{4}{9} \right) -\left( -\dfrac{4}{3} +\dfrac{4}{9} \right) \\ & = \underline{\dfrac{32}{9}} \end{align}\]

« 解答を隠す