解答はこちら »

【 解 答 】

(1)

\[ A = \sqrt{a^2+1} \left( \begin{array}{cc} \dfrac{a}{\sqrt{a^2+1}} & -\dfrac{1}{\sqrt{a^2+1}} \\ \dfrac{1}{\sqrt{a^2+1}} & \dfrac{a}{\sqrt{a^2+1}} \end{array} \right) \] なので \[ r= \underline{\sqrt{a^2+1}} , \ \cos \theta =\underline{\dfrac{a}{\sqrt{a^2+1}}} , \ \sin \theta =\underline{\dfrac{1}{\sqrt{a^2+1}}} \]

(2)

(1) の結果から, 点 P に対して, 点 \(\text{P}' =f(\text{P})\) は \[ \overrightarrow{\text{OP}'} = r \overrightarrow{\text{OP}} , \ \angle \text{POP}'= \theta \] を満たす.
\(\text{OQ} _ 1=1\) なので \[\begin{align} \text{OQ} _ n & = r^{n-1} , \ \text{OQ} _ {n+1} = r^n , \ \angle \text{Q} _ n\text{OQ} _ {n+1} = \theta \\ \text{∴} \quad S(n) & =\dfrac{1}{2} r^{2n-1} \sin \theta =\dfrac{1}{2} \left( \sqrt{a^2+1} \right)^{2n-1} \cdot \dfrac{1}{\sqrt{a^2+1}} \\ & = \underline{\dfrac{1}{2}(a^2+1)^{n-1}}\ \end{align}\]

(3)

条件より \[\begin{align} \left( \begin{array}{cc} a & -1 \\ 1 & a \end{array} \right) \left( \begin{array}{c} x \\ y \end{array} \right) & = \left( \begin{array}{c} 2 \\ 7 \end{array} \right) \\ \text{∴} \quad \left( \begin{array}{c} x \\ y \end{array} \right) & = \dfrac{1}{a^2+1}\left( \begin{array}{cc} a & -1 \\ 1 & a \end{array} \right) \left( \begin{array}{c} 2 \\ 7 \end{array} \right) \\ & = \dfrac{1}{a^2+1} \left( \begin{array}{c} 2a+7 \\ 7a-2 \end{array} \right) \end{align}\] この点の \(x\) 座標を四捨五入すると \(2\) となるので \[\begin{align} \dfrac{3}{2} & \leqq \dfrac{2a+7}{a^2+1} \lt \dfrac{5}{2} \\ 3a^2+3 & \leqq 4a+14 \lt 5a^2+5 \\ 3a^2-4a-11 & \leqq 0 \ \text{かつ} \ (5a-9)(a+1) \gt 0 \\ \dfrac{2-\sqrt{37}}{3} \leqq a & \leqq \dfrac{2+\sqrt{37}}{3} \ \text{かつ} \ a \lt -1 , \dfrac{9}{5} \lt a \end{align}\] \(a\) は整数であり, \(6 \lt \sqrt{37} \lt 7\) なので, \[\begin{align} -1 \leqq a \leqq 2 \ & \text{かつ} \ a \leqq -2 , 2 \leqq a \\ \text{∴} \quad a & = \underline{2} \end{align}\] このとき, (2) の結果より \[ S(n) = \dfrac{1}{2} \cdot 5^{n-1} = \dfrac{10^{n-1}}{2^n} \gt 10^{10} \] 両辺について常用対数をとると \[\begin{align} n-1-n \log _ {10} 2 & \gt 10 \\ \text{∴} \quad n & \gt \dfrac{11}{1 -\log _ {10} 2} \end{align}\] ここで, \(0.3 \lt \log _ {10} 2 \lt 0.31\) であり, \(\dfrac{11}{1-0.31} =15.9 \cdots\) なので \[ n \geqq 16 \] ゆえに, 最小の \(n\) は \[ n= \underline{16} \]

« 解答を隠す

解答はこちら »

【 解 答 】

線分 PQ は, \[ \dfrac{x}{8 \cos \theta} +\dfrac{y}{\sin \theta} = 1 \quad ( x \geqq 0 , \ y \geqq 0 ) \] と表せる. \(x=k \ ( 0 \leqq k \leqq 8 )\) と固定すると \[ y = \sin \theta -\dfrac{k \sin \theta}{8 \cos \theta} = \sin \theta -\dfrac{k}{8} \tan \theta \] \(y \geqq 0\) なので, \(\theta \ \left( 0 \leqq \theta \leqq \dfrac{\pi}{2} \right)\) の取りうる値の範囲は \[\begin{align} \sin \theta \left( 1-\dfrac{k}{8 \cos \theta} \right) & \geqq 0 \\ \text{∴} \quad \cos \theta \geqq \dfrac{k}{8} \quad & ( \ \text{∵} \ \sin \theta \geqq 0 \ ) \end{align}\] したがって \[ 0 \leqq \theta \leqq \theta _ 0 \quad \left( \cos \theta _ 0 = \dfrac{k}{8} \right) \] \(\theta\) がこの範囲を動くときの \(y\) の取りうる値の範囲を考える.
\(y = f( \theta )\) とおくと \[\begin{align} f'( \theta ) & = \cos \theta +\dfrac{k}{8 \cos^2 \theta} =\dfrac{8 \cos^3 \theta -k}{8 \cos^2 \theta} \\ & = \dfrac{\left( 2\cos \theta -k^{\frac{1}{3}} \right) \left( 4\cos^2 \theta +2 k^{\frac{1}{3}} \cos \theta +k^{\frac{2}{3}} \right)}{8 \cos^2 \theta} \end{align}\] \(f'( \theta ) =0\) を解くと \[ \cos \theta = \dfrac{k^{\frac{1}{3}}}{2} \] これを満たす \(\theta\) を \(\alpha\) とおけば, \(f( \theta )\) の増減表は下図のようになる. \[ \begin{array}{c|ccccc} \theta & 0 & \cdots & \alpha & \cdots & \theta _ 0 \\ \hline f'( \theta ) & & + & 0 & - & \\ \hline f( \theta ) & 0 & \nearrow & \text{最大} & \searrow & 0 \end{array} \] \[\begin{align} \sin \alpha & = \sqrt{1-\cos^2 \alpha} =\sqrt{1-\dfrac{k^{\frac{2}{3}}}{4}} , \\ \tan \alpha & = \dfrac{\sin \alpha}{\cos \alpha} =\dfrac{2}{k^{\frac{1}{3}}} \sqrt{1-\dfrac{k^{\frac{2}{3}}}{4}} \end{align}\] なので, \[\begin{align} f( \alpha ) & = \sqrt{1-\dfrac{k^{\frac{2}{3}}}{4}} -\dfrac{k}{8} \cdot \dfrac{2}{k^{\frac{1}{3}}} \sqrt{1-\dfrac{k^{\frac{2}{3}}}{4}} \\ & = \left( 1-\dfrac{k^{\frac{2}{3}}}{4} \right)^{\frac{3}{2}} \end{align}\] したがって \[ 0 \leqq f( \theta ) \leqq \left( 1-\dfrac{k^{\frac{2}{3}}}{4} \right)^{\frac{3}{2}} \] 以上より, 求める体積 \(V\) は \[\begin{align} V & = \pi \displaystyle\int _ 0^8 \left\{ f( \theta ) \right\}^2 \, dk =\pi \displaystyle\int _ 0^8 \left( 1-\dfrac{k^{\frac{2}{3}}}{4} \right)^3 \, dk \\ & = \pi \displaystyle\int _ 0^8 \left( 1 -\dfrac{3}{4}k^{\frac{2}{3}} +\dfrac{3}{16}k^{\frac{4}{3}} -\dfrac{1}{64}k^2 \right) \, dk \\ & = \pi \left[ k -\dfrac{3}{4} \cdot \dfrac{3}{5}k^{\frac{5}{3}} +\dfrac{3}{16} \cdot \dfrac{3}{7}k^{\frac{7}{3}} -\dfrac{1}{64} \cdot \dfrac{1}{3}k^3 \right] _ 0^8 \\ & = \pi \left( 8 -\dfrac{9 \cdot 2^5}{20} +\dfrac{9 \cdot 2^7}{16 \cdot 7} -\dfrac{2^9}{64 \cdot 3} \right) \\ & = \pi \left( 8 -\dfrac{72}{5} +\dfrac{72}{7} -\dfrac{8}{3} \right) \\ & = 8 \pi \left( 1 -\dfrac{9}{5} +\dfrac{9}{7} -\dfrac{1}{3} \right) \\ & = \underline{\dfrac{128 \pi}{105}} \end{align}\]

« 解答を隠す

解答はこちら »

【 解 答 】

(1)

\(y = f(x)\) が点 \(( 0 , 1 )\) を通るので \[\begin{align} f(0) & = p^2+q = 1 \\ \text{∴} \quad q & = 1-p^2 \quad ... [1] \end{align}\] また \(y=f(x)\) と \(y=x\) が \(x \gt 0\) の部分で接するので, \((x-p)^2+1-p^2 = x\) , すなわち, \(x^2-(2p+1)x+1 = 0 \ ... [2]\) が正の重解をもてばよい.
[2] の判別式 \(D\) について \[\begin{align} D = (2p+1)^2 -4 \cdot 1 & = 0 \\ 4p^2+4p-3 & = 0 \\ (2p-1)(2p+3) & = 0 \\ \text{∴} \quad p & = \dfrac{1}{2} , -\dfrac{3}{2} \end{align}\] 解と係数の関係より, \(2p+1 \gt 0\) つまり \(p \gt -\dfrac{1}{2}\) なので, \[ p = \dfrac{1}{2} \] [1] より \[ q = 1-\left( \dfrac{1}{2} \right)^2 =\dfrac{3}{4} \] ゆえに, 求める実数の組は \[ ( p , q ) = \underline{\left( \dfrac{1}{2} , \dfrac{3}{4} \right)} \] このときの接点の座標は, [2] について \[\begin{align} x^2-2x+1 & =0 \\ \text{∴} \quad x & =1 \end{align}\] 接点は \(y = x\) 上にあるので, \[ y=1 \] ゆえに, 接点の座標は \[ \underline{( 1 , 1 )} \]

(2)

\(g(x) = f _ 2(x) -f _ 1(x)\) とおくと, \(g(x)\) は \(x\) について, 高々 \(1\) 次の関数である.
条件より, \(g( \alpha ) \gt 0 , \ g( \beta ) \gt 0\) なので, \(\alpha \leqq x \leqq \beta\) において, \(g(x) \gt 0\) , すなわち, \(f _ 1(x) \lt f _ 2(x)\) .

(3)

(1) の場合の \(f(x)\) を \(f _ 0(x) = \left( x-\dfrac{1}{2} \right)^2 +\dfrac{3}{4}\) とおくと \[ f _ 0(0) = 1 , \ f _ 0(1) = 1 \quad ... [3] \] \(f(x)\) について, \(f(0) , f(1)\) の値によって場合分けして考える.

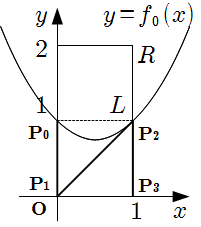
1. 1*　\(0 \leqq f(0) \leqq 1\) または \(0 \leqq f(1) \leqq 1\) のとき
   \(y=f(x)\) は, 線分 \(\text{P} _ 0\text{P} _ 1\) または \(\text{P} _ 2\text{P} _ 3\) で \(L\) と共有点をもつため, 不適.

2. 2*　「 \(f(0) \gt 1 , \ f(1) \lt 0\) 」または「 \(f(0) \lt 0 , \ f(1) \gt 1\) 」のとき
   \(y=f(x)\) は, 線分 \(\text{P} _ 1\text{P} _ 2\) で \(L\) と共有点をもつため, 不適.

3. 3*　\(f(0) \lt 0 , \ f(1) \lt 0\) のとき
   \(0 \leqq x \leqq 1\) において, \(y = f(x) \lt 0\) で, 領域 \(R\) を通過しないため, 不適.

4. 4*　\(f(0) \gt 1 , \ f(1) \gt 1\) のとき
   (2) の結果を用いれば, [3] より, \(0 \leqq x \leqq 1\) において, \(f(x) \gt f _ 0(x)\) .
   \(p = \dfrac{1}{2}\) と固定し, \(\dfrac{3}{4} \lt q \leqq 2\) と動かせば, \(y = f(x)\) は領域 \(R\) のうち \(y = f _ 0(x)\) より上側をすべて通過し, この部分が領域 \(T\) となる.

1*～4*より, 領域 \(S\) は, 領域 \(R\) のうち \(y = f _ 0(x)\) より下側で, 下図斜線部（境界を含む）となる.

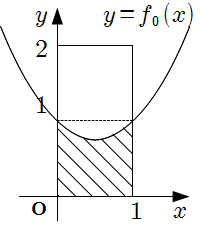
また, この部分の面積は \[\begin{align} \displaystyle\int _ 0^1 f _ 0(x) \, dx & = \displaystyle\int _ 0^1 (x^2-x+1) \, dx \\ & = \left[ \dfrac{x^3}{3} -\dfrac{x^2}{2} +x \right] _ 0^1 \\ & = \underline{\dfrac{5}{6}} \end{align}\]

« 解答を隠す

解答はこちら »

【 解 答 】

(1)

三角不等式, \(|x| \geqq 1\) を用いれば \[ | px+q | \leqq |px| +|q| \leqq |p|x +|q|x = \left( |p|+|q| \right) x \] なので, \(r = |p|+|q|\) とおけば \[ | px+q | \leqq rx \] が成立する.

(2)

\(\alpha -\beta = \dfrac{\alpha^3 -\beta^3}{\alpha^2 +\alpha \beta +\beta^2}\) であることを用いれば \[ \left| \sqrt[3]{f(x)} -x -k \right| = \left| \dfrac{f(x) -(x+k)^3}{\left\{ f(x) \right\}^{\frac{2}{3}} +(x+k) \left\{ f(x) \right\}^{\frac{1}{3}} +(x+k)^2} \right| \quad ... [1] \] ここで, \(k=\dfrac{a}{3}\) とおけば, [1]の分子は \[\begin{align} f(x) -(x+k)^3 & = x^3 +ax^2 +bx +c -\left( x+\dfrac{a}{3} \right)^3 \\ & = \left( b -\dfrac{a^2}{9} \right) x +c -\dfrac{a^3}{27} \end{align}\] また, \(a , b , c\) はすべて正なので \[ \left\{ f(x) \right\}^{\frac{1}{3}} \geqq x , \ x+k = x+\dfrac{a}{3} \geqq x \] したがって, [1] の分母は \[ \left\{ f(x) \right\}^{\frac{2}{3}} +(x+k) \left\{ f(x) \right\}^{\frac{1}{3}} +(x+k)^2 \geqq 3x^2 \geqq x^2 \] 以上を用いれば, \(p= b -\dfrac{a^2}{9}\) , \(q = c -\dfrac{a^3}{27}\) とおけば \[ [1] \leqq \left| \dfrac{px+q}{x^2} \right| \quad ... [1]' \]

(1) の結果を両辺 \(x^2\) で割れば \[ \left| \dfrac{px+q}{x^2} \right| \leqq \dfrac{r}{x} \] を満たす定数 \(r\) が存在するので, \(l=r\) とおけば \[ [1]' \leqq \dfrac{l}{x} \] となる \(l\) が存在することが示された.

(3)

(2) の結果と, \(\sqrt[3]{f(x)} \geqq x+\dfrac{a}{3}\) を用いれば \[ 0 \leqq \sqrt[3]{f(x)} -x -\dfrac{a}{3} \leqq \dfrac{l}{x} \quad ... [2] \] を満たす定数 \(l\) が存在する.
自然数 \(n\) を \(x\) に代入すると, \[ 0 \leqq \sqrt[3]{f(n)} -n -\dfrac{a}{3} \leqq \dfrac{l}{n} \] ここで, 両辺 \(n \rightarrow \infty\) のときを考えると, \(\displaystyle\lim _ {n \rightarrow \infty} \dfrac{l}{n} =0\) なので, はさみうちの原理から \[\begin{align} \displaystyle\lim _ {n \rightarrow \infty} \left( \sqrt[3]{f(n)} -n -\dfrac{a}{3} \right) & =0 \\ \text{∴} \quad \displaystyle\lim _ {n \rightarrow \infty} \left( \sqrt[3]{f(n)} -n \right) & = \dfrac{a}{3} \end{align}\] 条件より, 左辺は自然数なので, \(\dfrac{a}{3}\) も自然数となる.
[2] において, \(l\) より大きい \(4\) つの自然数 \(n _ k \ ( k=1, 2, 3, 4 )\) を代入すると \[\begin{align} \sqrt[3]{f(n _ k)} -n _ k & -\dfrac{a}{3} = 0 \\ \text{∴} \quad f(n _ k) & = \left( n _ k+\dfrac{a}{3} \right)^3 \end{align}\] \(f(n)\) は \(3\) つの定数をもつので, \(4\) つの変数について成立する恒等式 \[ f(n) = \left( n+\dfrac{a}{3} \right)^3 \] は任意の実数に対して成立する.
よって, 自然数 \(m = \dfrac{a}{3}\) とおくことで, 題意は示された.

« 解答を隠す

解答はこちら »

【 解 答 】

(1)

\(b _ n = a _ {n+1} -a _ n \ ( n= 2, 3, \cdots )\) とおくと \[ b _ n = r _ n b _ {n-1} , \ b _ 1 = a _ 2 -a _ 1 = r \] これを繰返し用いれば, \(n \geqq 2\) のとき \[ b _ n = r _ n \cdot r _ {n-1} \cdots r _ 2 \cdot r \] ここで, \(r _ 2, \cdots , r _ {n-1}\) の値の組合せは, \(2^{n-1}\) 通りあり同様に確からしい.
それぞれの場合における \(b _ n\) の値を \(c _ i \ ( i = 1 , \cdots , 2^{n-1} )\) とおけば, \(b _ n\) の期待値（すなわち \(p _ {n+1}-p _ n\) ）を \(q _ n\) とおけば, 二項定理を用いて \[\begin{align} q _ n & = p _ {n+1}-p _ n = \textstyle\sum\limits _ {i=1}^{2^{n-1}} \dfrac{c _ i}{2^{n-1}} \\ & = \dfrac{r}{2^{n-1}} \textstyle\sum\limits _ {k=0}^{n-1} {} _ {n-1} \text{C} {} _ k \left( \dfrac{r}{2} \right)^k \left( \dfrac{1}{2r} \right)^{n-1-k} \\ & = \dfrac{r}{2^{n-1}} \left( \dfrac{r}{2} +\dfrac{1}{2r} \right)^{n-1} \\ & = r \left( \dfrac{r}{4}+\dfrac{1}{4r} \right)^{n-1} \quad ... [1] \end{align}\] [1] を用いれば, \[\begin{align} p _ 3 & = p _ 2 +q _ 2 = a _ 2 +r \left( \dfrac{r}{4}+\dfrac{1}{4r} \right) \\ & = \underline{\dfrac{r^2}{4} +r +\dfrac{1}{4}} , \\ p _ 4 & = p _ 3 +q _ 3 = \dfrac{r^2}{4} +r +\dfrac{1}{4} +r \left( \dfrac{r}{4}+\dfrac{1}{4r} \right)^2 \\ & = \dfrac{r^2}{4} +r +\dfrac{1}{4} +r \left( \dfrac{r^2}{16} +\dfrac{1}{8} +\dfrac{1}{16r^2} \right) \\ & = \underline{\dfrac{r^3}{16} +\dfrac{r^2}{4} +\dfrac{9r}{8} +\dfrac{1}{4} +\dfrac{1}{16r}} \end{align}\]

(2)

[1] より, \(n \geqq 3\) について \[\begin{align} p _ n & = p _ 2 +\textstyle\sum\limits _ {k=2}^{n-1} q _ k \\ & = r \textstyle\sum\limits _ {k=1}^{n-1} \left( \dfrac{r}{4}+\dfrac{1}{4r} \right)^{k-1} \quad ... [2] \end{align}\] 数列 \(\{ q _ n \}\) の公比について \[\begin{align} \dfrac{r}{4} +\dfrac{1}{4r} & = 1 \\ r^2 -4r +1 & = 0 \\ \text{∴} \quad r & = 2 \pm \sqrt{3} \end{align}\] なので, 場合分けして考える.

1. 1*　\(r \neq 2 \pm \sqrt{3}\) のとき, [2]より \[ p _ n = r \cdot \dfrac{1-\left( \dfrac{r}{4}+\dfrac{1}{4r} \right)^{n-1}}{1-\left( \dfrac{r}{4}+\dfrac{1}{4r} \right)} \]

2. 2*　\(r = 2 \pm \sqrt{3}\) のとき, [2]より \[ p _ n = r(n-1) \]

1* 2*より \[ p _ n = \underline{\left\{ \begin{array}{ll} r \cdot \dfrac{1-\left( \dfrac{r}{4}+\dfrac{1}{4r} \right)^{n-1}}{1-\left( \dfrac{r}{4}+\dfrac{1}{4r} \right)} & ( r \neq 2 \pm \sqrt{3} \text{のとき} ) \\ r(n-1) & ( r = 2 \pm \sqrt{3} \text{のとき} ) \end{array} \right.} \]

(3)

\(p _ n\) が収束する条件は, \(r \gt 0\) なので \[\begin{gather} \dfrac{r}{4} +\dfrac{1}{4r} \lt 1 \\ \text{∴} \quad \underline{2-\sqrt{3} \lt r \lt 2+\sqrt{3}} \end{gather}\]

(4)

(3) の場合には, \[\begin{align} \displaystyle\lim _ {n \rightarrow \infty} p _ n & = \dfrac{r}{1-\left( \dfrac{r}{4}+\dfrac{1}{4r} \right)} \\ & = \dfrac{4}{-\dfrac{1}{r^2}+\dfrac{4}{r}-1} \\ & = \dfrac{4}{-\left( \dfrac{1}{r}-2 \right)^2 +3} \leqq \dfrac{4}{3} \end{align}\] 等号成立は \(\dfrac{1}{r} =2\) すなわち \(r=\dfrac{1}{2}\) のとき.
ゆえに, 求める最小値は \[ \underline{\dfrac{4}{3}} \]

« 解答を隠す