---

\(xy\) 平面上に \(4\) 点 \((0,0) , (4,0) , (4,4) , (0,4)\) を頂点とする正方形 \(K\) を考える. 点 \((1,2)\) を通る各直線に対して, その \(K\) に含まれる部分を \(l\) とおく.

1. (1)　\(l\) の長さの最大値と, それを与える直線の方程式を求めよ.

2. (2)　\(l\) の長さの最小値を求めよ.

---

【 解 答 】

(1)

\(l\) の長さを \(L\) とおく.

1. 1*　\(l : \ x = 1\) のとき \[ L = 4 \]

2. 2*　\(l : \ y = a(x-1)+2\) のとき
   \(K , l\) はともに直線 \(y=2\) について対称なので, \(a \geqq 0\) のときを考えればよい.

   1. (i)　\(0 \leqq a \lt \dfrac{2}{3}\) のとき, \(l\) は下図のようになるので 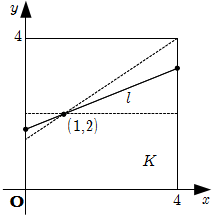\[ L = 4 \sqrt{a^2+1} \] この区間では \(L\) は単調増加である.

   2. (ii)　\(\dfrac{2}{3} \leqq a \lt 2\) のとき, \(l\) は下図のようになるので 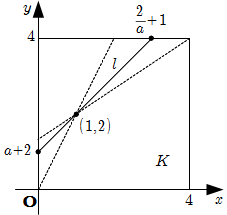\[\begin{align} L & = \sqrt{(a+2)^2 +\left( \dfrac{2}{a} +1 \right)^2} \\ & =(a+2) \sqrt{1+ \dfrac{1}{a^2}} \\ & = \left( 1+\dfrac{2}{a} \right) \sqrt{a^2+1} \end{align}\] したがって \[\begin{align} \dfrac{dL}{da} & = -\dfrac{2 \sqrt{a^2+1}}{a^2} +\dfrac{a+2}{a} \cdot \dfrac{a}{\sqrt{a^2+1}} \\ & = \dfrac{-2 ( a^2+1 ) +a^2 (a+2)}{a^2 \sqrt{a^2+1}} \\ & = \dfrac{a^3-2}{a^2 \sqrt{a^2+1}} \end{align}\] \(\dfrac{dL}{da} = 0\) をとくと \[ a = 2^{\frac{1}{3}} \]

   3. (iii)　\(a \geqq 2\) のとき, \(l\) は下図のようになるので 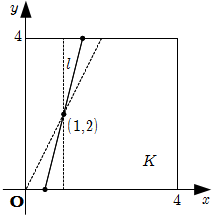\[ L = 4 \sqrt{1+\dfrac{1}{a^2}} \] この区間では \(L\) は単調減少である.

   (i) ～ (iii) から \(L\) の増減は下表のようになる. \[ \begin{array}{c|ccccccccc} a & 0 & \cdots & \dfrac{2}{3} & \cdots & 2^{\frac{1}{3}} & \cdots & 2 & \cdots & ( \infty ) \\ \hline \dfrac{dL}{da} & & & & - & 0 & + & & & \\ \hline L & 4 & \nearrow & \text{極大} & \searrow & \text{極小} & \nearrow & \text{極大} & \searrow & (4) \end{array} \]

1* 2* より, \(L\) の最大値の候補は

• \(a = \dfrac{2}{3}\) のとき \[ L = 4 \sqrt{\left( \dfrac{2}{3} \right)^2 +1} = \dfrac{4 \sqrt{13}}{3} \]

• \(a = 2\) のとき \[ L = \dfrac{4}{2} \sqrt{2^2+1} = 2 \sqrt{5} \]

ここで \[\begin{align} 52 & = 2^2 \cdot 13 \gt 3^2 \cdot 5 = 45 \\ \text{∴} \quad & \dfrac{4 \sqrt{13}}{3} \gt 2 \sqrt{5} \end{align}\] よって, 求める最大値は \[ \underline{\dfrac{4 \sqrt{13}}{3}} \] また, このときの \(l\) の式は, 対称性より \(a = \pm \dfrac{2}{3}\) のときなので \[\begin{gather} y = \pm \dfrac{2}{3} (x-1) +2 \\ \text{∴} \quad \underline{y = \dfrac{2}{3} x -\dfrac{4}{3} , \ y = -\dfrac{2}{3} x -\dfrac{8}{3}} \end{gather}\]

(2)

(1) の経過より, \(L\) の最小値の候補は

• \(a = 0\) のとき \[ L = 4 \]

• \(a = 2^{\frac{1}{3}}\) のとき \[\begin{align} L & = \left( 1 +\dfrac{2}{2^{\frac{1}{3}}} \right) \sqrt{2^{\frac{2}{3}} +1} \\ & = \left( 1+2^{\frac{2}{3}} \right)^{\frac{3}{2}} \end{align}\]

ここで \[\begin{align} \left( 1 -2^{\frac{1}{3}} \right)^2 & \gt 0 \\ 1 +2^{\frac{2}{3}} & \gt 2^{\frac{4}{3}} \\ \text{∴} \quad \left( 1+2^{\frac{2}{3}} \right)^{\frac{3}{2}} & \gt 2^{\frac{4}{3} \cdot \frac{3}{2}} = 4 \end{align}\] よって, 求める最小値は \[ \underline{4} \]