\(A _ 0 = \left( \begin{array}{cc} 0 & 0 \\ 0 & 0 \end{array} \right)\) とする. 整数 \(n \geqq 1\) に対して, 次の試行により行列 \(A _ {n-1}\) から行列 \(A _ n\) を定める.
この試行を \(n\) 回( \(n = 2 , 3 , 4 , \cdots\) )くり返した後に, \(A _ 0 , A _ 1 , \cdots , A _ {n-1}\) が逆行列をもたず \(A _ n\) は逆行列をもつ確率を \(p _ n\) とする.
【 解 答 】
(1)
\(n\) 回目に初めて \(|A _ n| \neq 0\) となる場合を考えればよい.
行, 列のいずれを入替えても, \(|A _ n|\) の値は変わらないので, \(1\) 回目には \(( 1 , 1 )\) が出ると考えても, 一般性を失わない.
\(p _ 2\) について, \(2\) 回目に \(( 2 , 2 )\) が出ればよいので
\[
p _ 2 = \underline{\dfrac{1}{4}}
\]
\(p _ 3\) について, \(3\) 回目に
\(A _ 2 = \left( \begin{array}{cc} 2 & 0 \\ 0 & 0 \end{array} \right)\) から \(( 2 , 2 )\)
\(A _ 2 = \left( \begin{array}{cc} 1 & 1 \\ 0 & 0 \end{array} \right)\) から \(( 2 , 1 )\) または \(( 2 , 2 )\)
\(A _ 2 = \left( \begin{array}{cc} 1 & 0 \\ 1 & 0 \end{array} \right)\) から \(( 1 , 2 )\) または \(( 2 , 2 )\)
が出ればよいので
\[
p _ 3 = \dfrac{1}{4} \cdot \dfrac{1}{4} +\dfrac{1}{4} \cdot \dfrac{1}{2} +\dfrac{1}{4} \cdot \dfrac{1}{2} =\underline{\dfrac{5}{16}}
\]
(2)
\(4\) 枚のうち, \(( 1 , 1 )\) , \(( 1 , 2 )\) の \(2\) 枚のみが出ればよい.
ただし, どちらか一方のみが出る場合は除くので,
\[
q _ {n-1} = \underline{\left( \dfrac{1}{2} \right)^{n-1} -2\left( \dfrac{1}{4} \right)^{n-1}}
\]
(3)
(1) と同様に, \(1\) 回目に \(( 1 , 1 )\) が出たとして考える.
\(|A _ {n-1}| =0\) となる行列は, 以下の \(3\) パターンがあり, それぞれに対して \(n\) 回目に
\(A _ {n-1} =\left( \begin{array}{cc} n-1 & 0 \\ 1 & 0 \end{array} \right)\) から \(( 2 , 2 )\)
\(A _ {n-1} =\left( \begin{array}{cc} n-1-k & k \\ 0 & 0 \end{array} \right) \quad ( 1 \leqq k \leqq n-2 )\) から \(( 2 , 1 )\) または \(( 2 , 2 )\)
\(A _ {n-1} =\left( \begin{array}{cc} n-1-k & 0 \\ k & 0 \end{array} \right) \quad ( 1 \leqq k \leqq n-2 )\) から \(( 1 , 2 )\) または \(( 2 , 2 )\)
が出ればよい.
よって
\[\begin{align}
p _ n & = \left( \dfrac{1}{4} \right)^{n-2} \cdot \dfrac{1}{4} +2 \left\{ \left( \dfrac{1}{2} \right)^{n-2} -\left( \dfrac{1}{4} \right)^{n-2} \right\} \cdot \dfrac{1}{2} \\
& = \underline{\left( \dfrac{1}{2} \right)^{n-2} -\dfrac{3}{4} \left( \dfrac{1}{4} \right)^{n-2}}
\end{align}\]
« 解答を隠す


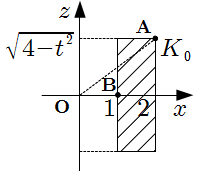 \[\begin{align}
\text{OA} & = \sqrt{(4-t^2)+2^2} = \sqrt{8-t^2} , \\
\text{OB} & = 1
\end{align}\]
したがって, \(L\) の断面積 \(T(t)\) は
\[
T(t)= ( \text{OA}^2-\text{OB}^2 ) \pi = (7-t^2) \pi
\]
\[\begin{align}
\text{OA} & = \sqrt{(4-t^2)+2^2} = \sqrt{8-t^2} , \\
\text{OB} & = 1
\end{align}\]
したがって, \(L\) の断面積 \(T(t)\) は
\[
T(t)= ( \text{OA}^2-\text{OB}^2 ) \pi = (7-t^2) \pi
\]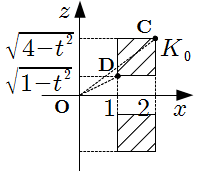 \[\begin{align}
\text{OC} & = \sqrt{(4-t^2)+2^2} = \sqrt{8-t^2} , \\
\text{OD} & = \sqrt{(1-t^2)+1^2} = \sqrt{2-t^2}
\end{align}\]
したがって, \(L\) の断面積 \(T(t)\) は
\[
T(t) = ( \text{OA}^2-\text{OB}^2 ) \pi = 6 \pi
\]
\[\begin{align}
\text{OC} & = \sqrt{(4-t^2)+2^2} = \sqrt{8-t^2} , \\
\text{OD} & = \sqrt{(1-t^2)+1^2} = \sqrt{2-t^2}
\end{align}\]
したがって, \(L\) の断面積 \(T(t)\) は
\[
T(t) = ( \text{OA}^2-\text{OB}^2 ) \pi = 6 \pi
\]