解答はこちら »

【 解 答 】

\(3\) 人でジャンケンをするとき, \(n\) 人（ \(n = 1 , 2\) ）が勝つ確率を \(t(n)\) , あいこになる確率を \(t(0)\) とおく.
\(3\) 人の手の出し方は, \(3^3 = 27\) 通りある.
\(n = 1 , 2\) のときについて, 勝つときの手はグー, チョキ, パーの \(3\) 通り, 勝つ人の選び方が \({} _ {3}\text{C} {} _ {n}\) 通りあるので \[ \begin{align} t(1) & = \dfrac{3 \cdot {} _ {3}\text{C} {} _ {1}}{3^3} = \dfrac{1}{3} \ , \\ t(2) & = \dfrac{3 \cdot {} _ {3}\text{C} {} _ {2}}{3^3} = \dfrac{1}{3} \ . \end{align} \] あいこになるのは, これら勝敗がつくときの余事象なので \[ t(0) = 1 -t(1) -t(2) = \dfrac{1}{3} \ . \] 続いて, \(2\) 人でジャンケンをするとき, 勝敗がつく（ \(1\) 人が勝つ）確率を \(d(1)\) , あいこになる確率を \(d(0)\) とおく.
同様に考えれば \[ \begin{align} d(1) & = \dfrac{3 \cdot {} _ {2}\text{C} {} _ {1}}{3^2} = \dfrac{2}{3} \ , \\ d(0) & = 1 -d(1) = \dfrac{1}{3} \ . \end{align} \]

(1)

\[ \begin{align} p_1 = t(2) = \underline{\dfrac{1}{3}} \ , \\ q_1 = t(0) = \underline{\dfrac{1}{3}} \ . \end{align} \]

(2)

\(n\) 回目終了時に \(3\) 人が残っている事象を P , \(2\) 人が残っている事象を Q , \(1\) 人が残っている事象を R とおくと, ジャンケンによる状態の遷移は下図のようになる.

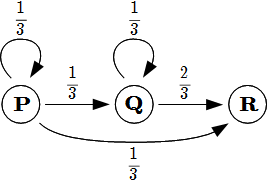
したがって, \(p_n , q_n\) がみたす漸化式は \[ \begin{align} & \left\{\begin{array}{l} p_{n+1} = d(0) p_n +t(2) q_{n} \\ q_{n+1} = t(0) q_n\end{array}\right. \\ \text{∴} \quad & \underline{\left\{\begin{array}{ll} p_{n+1} = \dfrac{1}{3} p_n +\dfrac{1}{3} q_{n} & \quad ... [1] \\ q_{n+1} = \dfrac{1}{3} q_n & \quad ... [2] \end{array}\right.} \ . \end{align} \] [2] と (1) の結果より, 数列 \(\{ q_n \}\) は, 初項 \(q_1 = \dfrac{1}{3}\) , 公比 \(\dfrac{1}{3}\) の等比数列なので \[ q_n = \underline{\dfrac{1}{3^n}} \ . \] これを [1] に代入すると \[ \begin{align} p_{n+1} = \dfrac{1}{3} p_n & +\dfrac{1}{3^{n+1}} \\ \text{∴} \quad 3^{n+1} p_{n+1} & = 3^n p_n +1 \ . \end{align} \] したがって, 数列 \(\{ 3^n p_n \}\) は, 初項 \(3 p_1 = 1\) , 公差 \(1\) の等差数列なので \[ \begin{align} 3^n p_n & = n \\ \text{∴} \quad p_n & = \underline{\dfrac{n}{3^n}} \ . \end{align} \]

(3)

\(1\) 回目で \(1\) 人が勝ち残るのは \[ t(1) = \dfrac{1}{3} \ . \] \(n\) 回目（ \(n \geqq 2\) ）で \(1\) 人が勝ち残るのは

• \(n-1\) 回目終了時点で, \(3\) 人が勝ち残り, \(n\) 回目で \(1\) 人が勝つとき

• \(n-1\) 回目終了時点で, \(2\) 人が勝ち残り, \(n\) 回目で \(1\) 人が勝つとき

の \(2\) 通りがあるので, 求める確率は \[ \begin{align} t(1) q_{n-1} +d(1) p_{n-1} & = \dfrac{1}{3} \cdot \dfrac{1}{3^{n-1}} +\dfrac{2}{3} \cdot \dfrac{n-1}{3^{n-1}} \\ & = \underline{\dfrac{2n-1}{3^n}} \ . \end{align} \] これは \(n=1\) のときも成立している.

« 解答を隠す

解答はこちら »

【 解 答 】

(1)

\(g(x) = \dfrac{100}{x}\) とおくと \[ f'(x) = g(x) \quad ... [1] \ . \] 実数 \(t \ ( t \gt 0 )\) について, \(t \lt x \lt t+1\) において \(g(x)\) は単調減少なので \[ g(t+1) \lt g(x) \lt g(t) \ . \] この区間で, 辺々を積分すると, [1] も用いて \[ \begin{align} g(t+1) & \lt \displaystyle\int_{t}^{t+1} g(x) \, dx \lt g(t) \\ \dfrac{100}{t+1} & \lt \left[ f(x) \right]_{t}^{t+1} \lt \dfrac{100}{t} \\ \text{∴} \quad \dfrac{100}{t+1} & \lt f(t+1) -f(t) \lt \dfrac{100}{t} \ . \end{align} \] よって, 題意は示された.

(2)

1. 1*　\(1 \leqq n \leqq 99\) のとき
   (1) の結果より \[ f(n+1) -f(n) \gt \dfrac{100}{99+1} = 1 \ . \] なので, \(\left[ f(n) \right]\) と \(\left[ f(n+1) \right]\) は必ず異なる整数となる.
   したがって, \([f(1)] , \cdots [f(99)]\) のうち, 異なるものの個数は \[ 99 \ \text{個} \ . \]

2. 2*　\(100 \leqq n \leqq 1000\) のとき
   (1) の結果より \[ f(n+1) -f(n) \lt \dfrac{100}{100} = 1 \ . \] なので, \(\left[ f(n) \right]\) と \(\left[ f(n+1) \right]\) は, 等しいか, 差が \(1\) であるか, のいずれかである. \[ \begin{align} [ f(100) ] & = [ 200 \log 10 ] = 460 \ , \\ [ f(1000) ] & = [ 300 \log 10 ] = 690 \ . \end{align} \] なので, \([f(100)] , \cdots , [f(1000)]\) は, \(460\) から \(690\) までの整数を漏れなく取りながら大きくなる.
   したがって, 異なるものの個数は \[ 690 -460 +1 = 231 \ \text{個} \ . \]

以上より, 求める個数は \[ 99 +231 = \underline{330} \ \text{個} \ . \]

« 解答を隠す

解答はこちら »

【 解 答 】

(1)

条件より \[ S_k(1) = 1 , \ S_k(2) = 1+2^k \] また \[\begin{align} \textstyle\sum\limits_{i=0}^m {} _ {m}\text{C} {} _ {i} & = (1+1)^m = 2^m \ , \\ \textstyle\sum\limits_{i=0}^m 2^i {} _ {m}\text{C} {} _ {i} & = (2+1)^m = 3^m \ . \end{align}\] なので, これらを用いれば \[ \begin{align} T_m(1) & = {} _ {m}\text{C} {} _ {1} S_1(1) + \cdots +{} _ {m}\text{C} {} _ {m-1} S_{m-1}(1) \\ & = \textstyle\sum\limits_{i=1}^{m-1} {} _ {m}\text{C} {} _ {i} \\ & = \textstyle\sum\limits_{i=0}^{m} {} _ {m}\text{C} {} _ {i} -\left( 1^m +1 \right) \\ & = \underline{2^m-2} \ , \\ T_m(2) & = {} _ {m}\text{C} {} _ {1} S_1(2) + \cdots +{} _ {m}\text{C} {} _ {m-1} S_{m-1}(2) \\ & = \textstyle\sum\limits_{i=1}^{m-1} {} _ {m}\text{C} {} _ {i} +\textstyle\sum\limits_{i=1}^{m-1} 2^{i} {} _ {m}\text{C} {} _ {i} \\ & = T_m(1) +\textstyle\sum\limits_{i=0}^{m} 2^{i} {} _ {m}\text{C} {} _ {i} -\left( 2^m +1 \right) \\ & = \underline{3^m-3} \ . \end{align} \]

(2)

(1) と同様に計算すれば \[ \begin{align} T_m(n) & = {} _ {m}\text{C} {} _ {1} S_1(n) + \cdots +{} _ {m}\text{C} {} _ {m-1} S_{m-1}(n) \\ & = \textstyle\sum\limits_{j=1}^{n} \textstyle\sum\limits_{i=1}^{m-1} j^{i} {} _ {m}\text{C} {} _ {i}\\ & = \textstyle\sum\limits_{j=1}^{n} \textstyle\sum\limits_{i=0}^{m} \left\{ j^{i} {} _ {m}\text{C} {} _ {i} -\left( j^m +1 \right) \right\} \\ & = \textstyle\sum\limits_{j=1}^{n} \left\{ (j+1)^m - j^m -1 \right\} \\ & = \left\{ (n+1)^m - n^m \right\} + \cdots + ( 2^m -1 ) -n\\ & = \underline{(n+1)^m -(n+1)} \ . \end{align} \]

(3)

(2) の結果について, \(n = p-1\) とおけば \[ T_{m}(p-1) = p^{p-1}-p \ . \] なので, 「 \(T_m(p-1)\) は \(p\) で割切れる. 」 ... [1] また, \(1 \leqq i \leqq p-1 , \ 1 \leqq j \leqq i\) をみたす自然数 \(i , j\) に対して, \(i !\) が \(p\) で割切れないので, 「 \({} _ {i}\text{C} {} _ {j} = \dfrac{i !}{i! ( i-j )!}\) は, \(p\) で割切れない. 」 ... [2] 以下では, 「 \(S_{k}(p-1)\) が \(p\) で割切れる. 」 ... [A] が \(k = 1 , 2 , \cdots , p-2\) で成立することを数学的帰納法を用いて示す.

1. 1*　\(k = 1\) のとき \[\begin{align} S_1(p-1) & = 1 +2 + \cdots +(p-1) \\ & = \dfrac{p(p-1)}{2} \ . \end{align}\] \(p\) は \(3\) 以上の素数なので, \(\dfrac{p-1}{2}\) は整数となり, \(S_1(p-1)\) は \(p\) で割切れる.
   つまり, \(k = 1\) のとき, [A] は成立する.

2. 2*　\(k = 1 , \cdots , \ell \ (1 \leqq \ell \leqq p-3 )\) のとき
   [A] が成立すると仮定すると \[\begin{align} T_{\ell +2} & (p-1) \\ & = \textstyle\sum\limits_{i=1}^{\ell +1} {} _ {\ell+2}\text{C} {} _ {i} S _ {i}(p-1) \\ & = \textstyle\sum\limits_{i=1}^{\ell} {} _ {\ell+2}\text{C} {} _ {i} S _ {i}(p-1) +{} _ {\ell+2}\text{C} {} _ {\ell +1} S _ {\ell +1}(p-1) \ . \end{align}\] ゆえに \[\begin{align} {} _ {\ell+2}\text{C} {} _ {\ell +1} & S _ {\ell +1}(p-1) = \\ & T _ {\ell +2} (p-1) -\textstyle\sum\limits_{i=1}^{\ell} {} _ {\ell+2}\text{C} {} _ {i} S _ {i}(p-1) \ . \end{align} \] [1] と仮定より右辺は \(p\) で割切れる.
   したがって, [2] より \(S_{\ell +1}(p-1)\) が \(p\) で割切れる.
   つまり, \(k = \ell +1\) のとき, [A] は成立する.

以上より, 題意は示された.

« 解答を隠す

解答はこちら »

【 解 答 】

(1)

時刻 \(t\) における \(C_1 , C_2\) の中心を P, \(C_1\) と \(x\) 軸の接点を T とおくと \[ \text{P} ( t , 1 ) , \ \text{T} ( t , 0 ) , \ \angle\text{TPA} = t \ . \] なので, 求める A の座標は \[ \left( x(t) , y(t) \right) = \underline{\left( t -2 \sin t , 1 -2\cos t \right)} \ . \]

(2)

(1) の結果より \[ \begin{align} x'(t) & = 1 -2\cos t \ , \\ y'(t) & = 2 \sin t \ . \end{align} \] \(x'(t) = 0\) をとくと \[ t = \dfrac{\pi}{3} , \dfrac{5 \pi}{3} \ . \] \(y'(t) = 0\) をとくと \[ t = 0 , \pi , 2 \pi \ . \] したがって, \(x , y\) の増減は下表のようになる. \[ \begin{array}{c|ccccccccc} t & 0 & \cdots & \frac{\pi}{3} & \cdots & \pi & \cdots & \frac{5 \pi}{3} & \cdots & 2 \pi\\ \hline x'(t) & & - & 0 & + & & + & 0 & - & \\ \hline y'(t) & 0 & + & & + & 0 & - & & - & 0 \\ \hline x(t) & 0 & \leftarrow & \frac{\pi}{3} -\sqrt{3} & \rightarrow & \pi & \rightarrow & \frac{5 \pi}{3} +\sqrt{3} & \leftarrow & 2 \pi \\ \hline y(t) & -1 & \uparrow & 0 & \uparrow & 3 & \downarrow & 0 & \downarrow & -1 \end{array} \\ \] 以上より, 求める A の座標は

• \(x(t)\) が最小になるとき, \(\underline{\left( \dfrac{\pi}{3} -\sqrt{3} , 0 \right)}\)

• \(x(t)\) が最大になるとき, \(\underline{\left( \dfrac{5 \pi}{3} +\sqrt{3} , 0 \right)}\)

• \(y(t)\) が最小になるとき, \(\underline{( 0 , -1 ) , \ ( 2 \pi , -1 )}\)

• \(y(t)\) が最大になるとき, \(\underline{( \pi , 3 )}\)

(3)

(2) の結果より, \(C\) と \(x\) 軸に囲まれた図形は下図のようになる.

よって, 求める面積 \(S\) は \[\begin{align} S & = \displaystyle\int_{\frac{\pi}{3} -\sqrt{3}}^{\frac{5 \pi}{3} +\sqrt{3}} y(t) \, dx \\ & = \displaystyle\int_{\frac{\pi}{3}}^{\frac{5 \pi}{3}} y(t) x'(t) \, dt \\ & = \displaystyle\int_{\frac{\pi}{3}}^{\frac{5 \pi}{3}} \left( 1 -2 \cos t \right)^2 \, dt \\ & = \displaystyle\int_{\frac{\pi}{3}}^{\frac{5 \pi}{3}} \left( 1 -4 \cos t +4 \cdot \dfrac{1 +\cos 2t}{2}\right) \, dt \\ & = \left[ 3t -4 \sin t +\sin 2t \right]_{\frac{\pi}{3}}^{\frac{5 \pi}{3}} \\ & = \underline{4 \pi +3 \sqrt{3}} \ . \end{align}\]

« 解答を隠す

解答はこちら »

【 解 答 】

(1)

\[\begin{align} A^2 & = \left( \begin{array}{cc} a & b \\ 0 & d \end{array} \right) \left( \begin{array}{cc} a & b \\ 0 & d \end{array} \right) \\ & = \left( \begin{array}{cc} a^2 & b(a+d) \\ 0 & d^2 \end{array} \right) \ . \end{align}\] \(A^2 = E\) なので, 成分を比較すれば \[ \left\{ \begin{array}{l} a^2 = d^2 = 1 \quad ... [1] \\ b(a+d) = 0 \quad ... [2] \end{array} \right. \ . \] [2] より \[ b = 0 \ \text{または} \ a+d = 0 \ . \]

1. 1*　\(b = 0\) のとき
   [1] より \[ a = \pm 1 , \ d = \pm 1 \ . \]

2. 2*　\(a+d = 0\) のとき
   [1] より \[ (a,d) = ( \pm 1 , \mp 1 ) \quad ( \text{複号同順} ) \ . \]

以上より, 求める \(A\) は \[\begin{align} A = & \underline{\left( \begin{array}{cc} \pm 1 & 0 \\ 0 & \pm 1 \end{array} \right) \quad ( \text{複号任意} ) , }\\ & \underline{\left( \begin{array}{cc} \pm 1 & k \\ 0 & \mp 1 \end{array} \right) \quad ( \text{複号同順} , \ k \text{は任意の実数} )} \ . \end{align}\]

(2)

\[\begin{align} A^3 & = \left( \begin{array}{cc} a^2 & b(a+d) \\ 0 & d^2 \end{array} \right) \left( \begin{array}{cc} a & b \\ 0 & d \end{array} \right) \\ & = \left( \begin{array}{cc} a^3 & b( a^2+ad+d^2 ) \\ 0 & d^3 \end{array} \right) \ . \end{align}\] \(A^3 = E\) なので, 成分を比較すれば \[ \left\{ \begin{array}{l} a^3 = d^3 = 1 \quad ... [3] \\ b(a^2+ad+d^2) = 0 \quad ... [4] \end{array} \right. \ . \] \(a ,d\) は実数なので, [3] より \[ a=d=1 \ . \] [4] に代入して \[\begin{align} 3b & = 0 \\ \text{∴} \quad b & = 0 \ . \end{align}\] よって求める \(A\) は \[ A = \underline{\left( \begin{array}{cc} 1 & 0 \\ 0 & 1 \end{array} \right)} \ . \]

(3)

\[\begin{align} A^4 & = \left( \begin{array}{cc} a^3 & b( a^2+ad+d^2 ) \\ 0 & d^3 \end{array} \right) \left( \begin{array}{cc} a & b \\ 0 & d \end{array} \right) \\ & = \left( \begin{array}{cc} a^4 & b( a^3+a^2d+ad^2+d^3 ) \\ 0 & d^4 \end{array} \right) \ . \end{align}\] \(A^4 = E\) なので, 成分を比較すれば \[ \left\{ \begin{array}{l} a^4 = d^4 = 1 \quad ... [5] \\ b( a^3+a^2d+ad^2+d^3 ) = 0 \quad ...[6] \end{array} \right. \ . \] \(a ,d\) は実数なので, [5] より \[ a^2 = d^2 = 1 \quad ... [7] \ . \] [7] を [6] に代入すると \[\begin{align} b ( a+d+a+d ) & = 0 \\ \text{∴} \quad b(a+d) & = 0 \quad ... [8] \ . \end{align}\] [7] かつ [8] は, [1] かつ [2] と等しい.
よって, \(A^4 = E\) をみたす \(A\) は, (1) の結果と等しく, すなわち \(A^2 = E\) をみたす.

« 解答を隠す

解答はこちら »

【 解 答 】

(1)

\[ f'(x) = 6x^2 -6x = 6x(x-1) \ . \] \(f'(x)=0\) をとくと \[ x = 0 , 1 \ . \] したがって, \(f(x)\) の増減は下表のようになる. \[ \begin{array}{c|ccccc} x & \cdots & 0 & \cdots & 1 & \cdots \\ \hline f'(x) & + & 0 & - & 0 & + \\ \hline f(x) & \nearrow & 1 & \searrow & 0 & \nearrow \end{array} \ . \] よって, \(y = f(x)\) のグラフは下図のようになる.

(2)

\(y = f(x)\) のグラフの形から, \(f(x) = a\) が相異なる \(3\) つの実数解をもつのは \[ 0 \lt a \lt 1 \quad ... [1] \ . \] の範囲であり \[ -\dfrac{1}{2} \lt \alpha \lt 0 \lt \beta \lt 1 \lt \gamma \lt \dfrac{3}{2} \quad ... [2] \ . \] \(f(x)= a\) を変形すると \[ 2x^3 -3x^2 -a+1 = 0 \ . \] なので, 解と係数の関係より \[\begin{align} \alpha +\beta +\gamma & = \dfrac{3}{2} \quad ... [3] , \\ \alpha \beta +\beta \gamma +\gamma \alpha & = 0 \quad ... [4] \ . \end{align}\] [3] より \[ \alpha +\gamma = \dfrac{3}{2} -\beta \ . \] これを [4] に代入すると \[\begin{align} \alpha \gamma & +\beta \left( \dfrac{3}{2} -\beta \right) = 0 \\ \text{∴} \quad \alpha \gamma & = -\beta \left( \dfrac{3}{2} -\beta \right) \ . \end{align}\] これらを用いれば \[\begin{align} \ell & = \sqrt{( \alpha +\gamma )^2 -4 \alpha \gamma} \\ & = \sqrt{\left( \dfrac{3}{2} -\beta \right)^2 +4 \beta \left( \dfrac{3}{2} -\beta \right)} \\ & = \sqrt{-3 \beta^2 +3 \beta +\dfrac{9}{4}} \\ & = \underline{\dfrac{1}{2} \sqrt{3 ( 3+ 4 \beta -4 \beta^2 )}} \ . \end{align}\]

(3)

[2] より, \(0 \lt \beta \lt 1\) であり \[ \ell = \sqrt{-3 \left( \beta -\dfrac{1}{2} \right)^2 +3} \ . \] なので, \(\ell\) の取りうる値の範囲は \[ \underline{\dfrac{3}{2} \lt \ell \leqq \sqrt{3}} \ . \]

« 解答を隠す

解答はこちら »

【 解 答 】

\[\begin{align} \displaystyle\int _ {a _ n}^{a _ {n+1}} \dfrac{dx}{\sqrt[3]{x}} & = \left[ \dfrac{3}{2} x^{\frac{2}{3}} \right] _ {a _ n}^{a _ {n+1}} \\ & = \dfrac{3}{2} \left( {a _ {n+1}}^{\frac{2}{3}} -{a _ n}^{\frac{2}{3}} \right) \ . \end{align}\] なので, 条件より \[\begin{align} \dfrac{3}{2} \left( {a _ {n+1}}^{\frac{2}{3}} -{a _ n}^{\frac{2}{3}} \right) & = 1 \\ \text{∴} \quad {a _ {n+1}}^{\frac{2}{3}} & = {a _ n}^{\frac{2}{3}} +\dfrac{2}{3} \ . \end{align}\] したがって, 数列 \(\left\{ {a _ n}^{\frac{2}{3}} \right\}\) は初項 \({a _ 1}^{\frac{2}{3}} = 1\) , 公差 \(\dfrac{2}{3}\) の等差数列なので \[ {a _ n}^{\frac{2}{3}} = 1 +\dfrac{2}{3} (n-1) = \dfrac{2n-1}{3} \quad ... [1] \ . \] また \[\begin{align} V _ x & = \pi \displaystyle\int _ {a _ n}^{a _ {n+1}} \left( \dfrac{1}{\sqrt[3]{x}} \right)^2 \, dx \\ & = \pi \left[ 3 x^{\frac{1}{3}} \right] _ {a _ n}^{a _ {n+1}} \\ & = 3 \pi \left( {a _ {n+1}}^{\frac{1}{3}} -{a _ n}^{\frac{1}{3}} \right) \ . \end{align}\] これと [1] を用いれば \[\begin{align} \sqrt{n} V _ x & = 3 \pi \sqrt{n} \left( \sqrt{\dfrac{2n+1}{3}} -\sqrt{\dfrac{2n-1}{3}} \right) \\ & = \sqrt{3n} \pi \cdot \dfrac{2}{\sqrt{2n+1} +\sqrt{2n-1}} \\ & = \dfrac{2 \sqrt{3} \pi}{\sqrt{2 +\frac{1}{n}} +\sqrt{2 -\frac{1}{n}}} \\ & \rightarrow \dfrac{2 \sqrt{3} \pi}{2 \sqrt{2}} \quad ( \ n \rightarrow \infty \text{のとき} ) \\ & = \dfrac{\sqrt{6}}{2} \pi \ . \end{align}\] よって \[ \displaystyle\lim _ {n \rightarrow \infty} \sqrt{n} V _ x = \underline{\dfrac{\sqrt{6}}{2} \pi} \ . \]

« 解答を隠す