名古屋大理系2009:第2問
関数 \(f(x)\) と \(g( \theta )\) を \[\begin{align} f(x) & = \displaystyle\int _ {-1}^x \sqrt{1-t^2} \, dt \quad ( -1 \leqq x \leqq 1 ) , \\ g( \theta ) & = f( \cos \theta ) -f( \sin \theta ) \quad ( 0 \leqq \theta \leqq 2\pi ) \end{align}\] で定める.
(1) 導関数 \(g'( \theta )\) を求めよ.
(2) \(g( \theta )\) を求めよ.
(3) \(y = g( \theta )\) のグラフをかけ.
【 解 答 】
(1)
\(f'(x) = \sqrt{1-x^2}\) なので \[\begin{align} g'( \theta ) & = -\sin \theta f' \left( \cos \theta \right) -\cos \theta f' \left( \sin \theta \right) \\ & = -\sin \theta \big| \sin \theta \big| -\cos \theta \big| \cos \theta \big| \end{align}\] \(\sin \theta , \cos \theta\) の正負に注意して, 場合分けすれば \[ g'( \theta )= \underline{\left\{ \begin{array}{ll} -1 & \ \left( 0 \leqq \theta \lt \dfrac{\pi}{2} \text{のとき} \right) \\ \cos 2\theta & \ \left( \dfrac{\pi}{2} \leqq \theta \lt \pi \text{のとき} \right) \\ 1 & \ \left( \pi \leqq \theta \lt \dfrac{3 \pi}{2} \text{のとき} \right) \\ -\cos 2\theta & \ \left( \dfrac{3 \pi}{2} \leqq \theta \leqq 2 \pi \text{のとき} \right) \end{array} \right.} \]
(2)
(1) の結果より
\[
g( \theta ) = \left\{ \begin{array}{ll} -\theta +C _ 1 & \ \left( 0 \leqq \theta \lt \dfrac{\pi}{2} \text{のとき} \right) \\ \dfrac{1}{2}\sin 2\theta +C _ 2 & \ \left( \dfrac{\pi}{2} \leqq \theta \lt \pi \text{のとき} \right) \\ \theta +C _ 3 & \ \left( \pi \leqq \theta \lt \dfrac{3 \pi}{2} \text{のとき} \right) \\ -\dfrac{1}{2} \sin 2\theta +C _ 4 & \ \left( \dfrac{3 \pi}{2} \leqq \theta \leqq 2 \pi \text{のとき} \right) \end{array} \right.
\]
ただし, \(C _ 1 , C _ 2 , C _ 3 , C _ 4\) は積分定数.
ここで, \(f(x)\) の値は半径 \(1\) の半円の面積に着目すれば

\[ f(-1) = 0 , \ f(0) = \dfrac{\pi}{4} , \ f(1) = \dfrac{\pi}{2} \] なので \[\begin{align} g(0) & = f(1) -f(0) = \dfrac{\pi}{4} = 0+C _ 1 \\ & \text{∴} \quad C _ 1 = \dfrac{\pi}{4} \\ g \left( \dfrac{\pi}{2} \right) & = f(0) -f(1) = -\dfrac{\pi}{4} = 0+C _ 2 \\ & \text{∴} \quad C _ 2 = -\dfrac{\pi}{4} \\ g \left( \pi \right) & = f(-1) -f(0) = -\dfrac{\pi}{4} = \pi +C _ 3 \\ & \text{∴} \quad C _ 3 = -\dfrac{5 \pi}{4} \\ g \left( \dfrac{3 \pi}{2} \right) & = f(0) -f(-1) = \dfrac{\pi}{4} = 0+C _ 4 \\ & \text{∴} \quad C _ 4 = -\dfrac{\pi}{4} \end{align}\] よって \[ g( \theta ) = \underline{\left\{ \begin{array}{ll} -\theta +\dfrac{\pi}{4} & \ \left( 0 \leqq \theta \lt \dfrac{\pi}{2} \text{のとき} \right) \\ \dfrac{1}{2}\sin 2\theta -\dfrac{\pi}{4} & \ \left( \dfrac{\pi}{2} \leqq \theta \lt \pi \text{のとき} \right) \\ \theta -\dfrac{5 \pi}{4} & \ \left( \pi \leqq \theta \lt \dfrac{3 \pi}{2} \text{のとき} \right) \\ -\dfrac{1}{2} \sin 2\theta -\dfrac{\pi}{4} & \ \left( \dfrac{3 \pi}{2} \leqq \theta \leqq 2 \pi \text{のとき} \right) \end{array} \right.} \]
(3)
(2) の結果より, グラフは下図のようになる.

- 投稿者:roundown
- 投稿公開日:2011/12/02
- 投稿カテゴリー:名古屋大理系2009


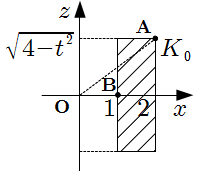 \[\begin{align}
\text{OA} & = \sqrt{(4-t^2)+2^2} = \sqrt{8-t^2} , \\
\text{OB} & = 1
\end{align}\]
したがって, \(L\) の断面積 \(T(t)\) は
\[
T(t)= ( \text{OA}^2-\text{OB}^2 ) \pi = (7-t^2) \pi
\]
\[\begin{align}
\text{OA} & = \sqrt{(4-t^2)+2^2} = \sqrt{8-t^2} , \\
\text{OB} & = 1
\end{align}\]
したがって, \(L\) の断面積 \(T(t)\) は
\[
T(t)= ( \text{OA}^2-\text{OB}^2 ) \pi = (7-t^2) \pi
\]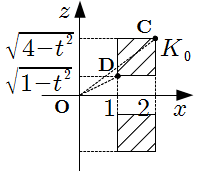 \[\begin{align}
\text{OC} & = \sqrt{(4-t^2)+2^2} = \sqrt{8-t^2} , \\
\text{OD} & = \sqrt{(1-t^2)+1^2} = \sqrt{2-t^2}
\end{align}\]
したがって, \(L\) の断面積 \(T(t)\) は
\[
T(t) = ( \text{OA}^2-\text{OB}^2 ) \pi = 6 \pi
\]
\[\begin{align}
\text{OC} & = \sqrt{(4-t^2)+2^2} = \sqrt{8-t^2} , \\
\text{OD} & = \sqrt{(1-t^2)+1^2} = \sqrt{2-t^2}
\end{align}\]
したがって, \(L\) の断面積 \(T(t)\) は
\[
T(t) = ( \text{OA}^2-\text{OB}^2 ) \pi = 6 \pi
\]