\(xy\) 平面上の放物線 \(y = x^2\) を \(C\) とする. 以下の問に答えよ.

1. (1)　\(C\) 上の点 \(( a , a^2 )\) における \(C\) の法線の方程式を求めよ.

2. (2)　点 \(( 1 , 2 )\) を通る \(C\) の法線の数を求めよ.

3. (3)　点 \(\left( t , t +\dfrac{1}{2} \right)\) を通る \(C\) の法線の数が \(2\) となるための \(t\) に対する条件を求めよ.

\(xy\) 平面上の円 \(C : \ x^2+y^2 = 1\) の内側を半径 \(\dfrac{1}{2}\) の円 \(D\) が \(C\) に接しながらすべらずに転がる. 時刻 \(t\) において \(D\) は点 \(( \cos t , \sin t )\) で \(C\) に接しているとする. \(D\) の周上の点 P の軌跡について考える. ある時刻 \(t _ 0\) において点 P が \(\left( \dfrac{1}{4} , \dfrac{\sqrt{3}}{4} \right)\) にあり, \(D\) の中心が第 \(2\) 象限にあるとする. 以下の問に答えよ.

1. (1)　時刻 \(t _ 0\) における \(D\) の中心の座標を求めよ.

2. (2)　第 \(1\) 象限において, 点 P が \(C\) 上にあるときの P の座標を求めよ.

3. (3)　点 P の軌跡を \(xy\) 平面上に図示せよ.

\(f(x) = \dfrac{\log x}{x}\) とする. 以下の問に答えよ.

1. (1)　\(y = f(x)\) のグラフの概形を次の点に注意して描け： \(f(x)\) の増減, グラフの凹凸, \(x \rightarrow +0\) , \(x \rightarrow \infty\) のときの \(f(x)\) の挙動.

2. (2)　\(n\) を自然数とする. \(k = 1 , 2 , \cdots , n\) に対して \(x\) が \(e^{\frac{k-1}{n}} \leqq x \leqq e^{\frac{k}{n}}\) を動くときの \(f(x)\) の最大値を \(M _ k\) , 最小値を \(m _ k\) とし, \[\begin{align} A _ n & = \textstyle\sum\limits _ {k=1}^n M _ k \left( e^{\frac{k}{n}} -e^{\frac{k-1}{n}} \right) \\ B _ n & = \textstyle\sum\limits _ {k=1}^n m _ k \left( e^{\frac{k}{n}} -e^{\frac{k-1}{n}} \right) \end{align}\] とおく. \(A _ n , B _ n\) を求めよ.

3. (3)　\(\displaystyle\lim _ {n \rightarrow \infty} A _ n , \ \displaystyle\lim _ {n \rightarrow \infty} B _ n\) を求めよ.

4. (4)　各 \(n\) に対して \(B _ n \lt \displaystyle\int _ 1^e f(x) \, dx \lt A _ n\) であることを示せ.

\(xy\) 平面上の原点を O とし, 楕円 \(\dfrac{x^2}{a^2} +\dfrac{y^2}{b^2} = 1 \ ( a \gt b \gt 0 )\) を \(E\) とする. \(E\) 上の点 P \(( s , t )\) における \(E\) の法線と \(x\) 軸との交点を Q とする. 点 P が \(s \gt 0 , \ t \gt 0\) の範囲を動くとき, \(\angle \text{OPQ}\) が最大になる点 P を求めよ.

四面体 OABC において \(\text{OA} = \text{BC} = 2\) , \(\text{OB} = 3\) , \(\text{OC} = \text{AB} = 4\) , \(\text{AC} = 2 \sqrt{6}\) である. また, \(\overrightarrow{a} = \overrightarrow{\text{OA}}\) , \(\overrightarrow{b} = \overrightarrow{\text{OB}}\) , \(\overrightarrow{c} = \overrightarrow{\text{OC}}\) とする. 以下の問に答えよ.

1. (1)　内積 \(\overrightarrow{a} \cdot \overrightarrow{b}\) , \(\overrightarrow{a} \cdot \overrightarrow{c}\) , \(\overrightarrow{b} \cdot \overrightarrow{c}\) を求めよ.

2. (2)　\(\triangle \text{OAB}\) を含む平面を \(H\) とする. \(H\) 上の点 P で直線 PC と \(H\) が直交するものをとる. このとき, \(\overrightarrow{\text{OP}} = x \overrightarrow{a} +y \overrightarrow{b}\) となる \(x , y\) を求めよ.

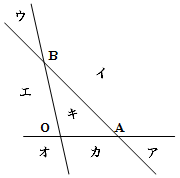
3. (3)　平面 \(H\) を直線 OA , AB , BO で下図のように \(7\) つの領域ア, イ, ウ, エ, オ, カ, キにわける. 点 P はどの領域に入るか答えよ.


4. (4)　辺 AB で △ABC と △OAB のなす角は鋭角になるか, 直角になるか, それとも鈍角になるかを判定せよ. ただし, \(1\) 辺を共有する \(2\) つの三角形のなす角とは, 共有する辺に直交する平面での \(2\) つの三角形の切り口のなす角のことである.