\(a\) を正の実数とし, 空間内の \(2\) つの円板 \[\begin{align} D _ 1 & = \big\{ (x, y, z) \big| x^2+y^2 \leqq 1 , z=a \big\} , \\ D _ 2 & = \big\{ (x, y, z) \big| x^2+y^2 \leqq 1 , z=-a \big\} \end{align}\] を考える. \(D _ 1\) を \(y\) 軸のまわりに \(180^{\circ}\) 回転して \(D _ 2\) に重ねる. ただし回転は \(z\) 軸の正の部分を \(x\) 軸の正の方向に傾ける向きとする. この回転の間に \(D _ 1\) が通る部分を \(E\) とする. \(E\) の体積を \(V(a)\) とし, \(E\) と \(\big\{ (x, y, z) \big| x \geqq 0 \big\}\) との共通部分の体積を \(W(a)\) とする.

1. (1)　\(W(a)\) を求めよ.

2. (2)　\(\displaystyle\lim _ {a \rightarrow \infty} V(a)\) を求めよ.

1. (1)　実数 \(x\) が \(-1 \lt x \lt 1\) , \(x \neq 0\) をみたすとき, 次の不等式を示せ. \[ (1-x)^{1-\frac{1}{x}} \lt (1+x)^{\frac{1}{x}} \]

2. (2)　次の不等式を示せ. \[ 0.9999^{101} \lt 0.99 \lt 0.9999^{100} \]

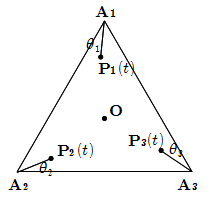
平面上の \(2\) 点 P , Q の距離を \(d( \text{P} , \text{Q} )\) と表すことにする. 平面上に点 O を中心とする一辺の長さが \(1000\) の正三角形 \(\triangle \text{A} {} _ 1 \text{A} {} _ 2 \text{A} {} _ 3\) がある. \(\triangle \text{A} {} _ 1 \text{A} {} _ 2 \text{A} {} _ 3\) の内部に \(3\) 点 \(\text{B} {} _ 1 , \text{B} {} _ 2 , \text{B} {} _ 3\) を, \(d( \text{A} {} _ n , \text{B} {} _ n ) = 1 \quad ( n=1, 2, 3 ) \) となるようにとる. また, \[\begin{align} \overrightarrow{a _ 1} & = \overrightarrow{\text{A} {} _ 1 \text{A} {} _ 2} , \quad \overrightarrow{a _ 2} = \overrightarrow{\text{A} {} _ 2 \text{A} {} _ 3} , \quad \overrightarrow{a _ 3} = \overrightarrow{\text{A} {} _ 3 \text{A} {} _ 1} , \\ \overrightarrow{e _ 1} & = \overrightarrow{\text{A} {} _ 1 \text{B} {} _ 1} , \quad \overrightarrow{e _ 2} = \overrightarrow{\text{A} {} _ 2 \text{B} {} _ 2} , \quad \overrightarrow{e _ 3} = \overrightarrow{\text{A} {} _ 3 \text{B} {} _ 3} \end{align}\] とおく. \(n=1, 2, 3\) のそれぞれに対して, 時刻 \(0\) に \(\text{A} {} _ n\) を出発し, \(\overrightarrow{e _ n}\) の向きに速さ \(1\) で直進する点を考え, 時刻 \(t\) におけるその位置を \(\text{P} {} _ n (t)\) と表すことにする.

1. (1)　ある時刻 \(t\) で \(d( \text{P} {} _ 1 (t) , \text{P} {} _ 2 (t) ) \leqq 1\) が成立した. ベクトル \(\overrightarrow{e _ 1}-\overrightarrow{e _ 2}\) と, ベクトル \(\overrightarrow{a _ 1}\) とのなす角を \(\theta\) とおく. このとき \(| \sin \theta | \leqq \dfrac{1}{1000}\) となることを示せ.

2. (2)　角度 \(\theta _ 1 , \theta _ 2 , \theta _ 3\) を \(\theta _ 1 = \angle \text{B} {} _ 1 \text{A} {} _ 1 \text{A} {} _ 2\) , \(\theta _ 2 = \angle \text{B} {} _ 2 \text{A} {} _ 2 \text{A} {} _ 3\) , \(\theta _ 3 = \angle \text{B} {} _ 3 \text{A} {} _ 3 \text{A} {} _ 1\) によって定義する. \(\alpha\) を \(0 \lt \alpha \lt \dfrac{\pi}{2}\) かつ \(\sin \alpha =\dfrac{1}{1000}\) をみたす実数とする. (1) と同じ仮定のもとで, \(\theta _ 1 +\theta _ 2\) の値のとる範囲を \(\alpha\) を用いて表せ.

3. (3)　時刻 \(t _ 1 , t _ 2 , t _ 3\) のそれぞれにおいて, 次が成立した. \[ d(\text{P} {} _ 2 (t _ 1) , \text{P} {} _ 3 (t _ 1)) \leqq 1 , \quad d(\text{P} {} _ 3 (t _ 2) , \text{P} {} _ 1 (t _ 2)) \leqq 1 , \quad d(\text{P} {} _ 1 (t _ 3) , \text{P} {} _ 2 (t _ 3)) \leqq 1 \] このとき, 時刻 \(T =\dfrac{1000}{\sqrt{3}}\) において同時に \[ d(\text{P} {} _ 1 (T) , \text{O}) \leqq 3 , \quad d(\text{P} {} _ 2 (T) , \text{O}) \leqq 3 , \quad d(\text{P} {} _ 3(T) , \text{O}) \leqq 3 \] が成立することを示せ.