\(a\) を正の実数とする.
点 \((x,y)\) が, 不等式 \(x^2 \leqq y \leqq x\) の定める領域を動くとき, 常に \(\dfrac{1}{2} \leqq (x-a)^2+y \leqq 2\) となる. \(a\) の範囲を求めよ.
解答
\(x^2 \leqq y \leqq x\) ... [1] が示す領域 \(D\) は, 下図斜線部.

\(\dfrac{1}{2} \leqq (x-a)^2+y \leqq 2\) ... [2] を変形すると
\[
-(x-a)^2 +\dfrac{1}{2} \leqq y \leqq -(x-a)^2 +2
\]
ゆえに, [2] が示す領域 \(C\) は \(2\) つの放物線に挟まれた下図斜線部.
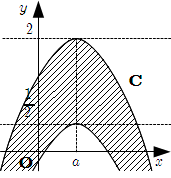
以上より, \(D\) が \(C\) が含まれるような, \(a\) の範囲を求めればよい.
\(a\) すなわち \(C\) を作る \(2\) つの放物線を動かすとき, \(D\) を含むかどうかの境界となるのは, 以下の \(2\) つの場合が考えられる.
1* 下の放物線が, \(0 \leqq x \leqq 1\) で \(y=x^2\) と接するとき.
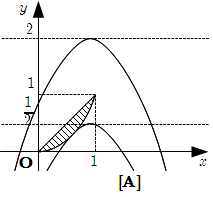
2* 上の放物線の \(x \leqq a\) の部分が, 原点を通るとき.
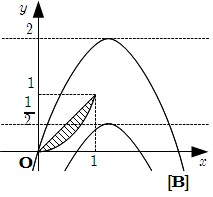
それぞれの場合の \(a\) の値を求める.
1*について
\[\begin{align}
-(x-a)^2+\dfrac{1}{2} & =x^2 \\
4x^2 -4ax +2a^2 -1 & = 0
\end{align}\]
この判別式 \(E\) について
\[\begin{align}
E = (2a)^2 -4 \left( 2a^2 -1 \right) & = 0 \\
4a^2 -4 & = 0 \\
\text{∴} \quad a = 1
\end{align}\]
2*について
\[\begin{align}
0 = -(0-a)^2 & +2 \\
\text{∴} \quad a & = \sqrt{2}
\end{align}\]
よって, 求める \(a\) の範囲は
\[
\underline{1 \leqq a \leqq \sqrt{2}}
\]



