原点 O \((0,0)\) を中心とする半径 \(1\) の円に, 円外の点 P \(( x _ 0 , y _ 0 )\) から \(2\) 本の接線を引く.

1. (1)　\(2\) つの接点の中点を Q とするとき, 点 Q の座標 \(( x _ 1 , y _ 1 )\) を点 P の座標 \(( x _ 0 , y _ 0 )\) を用いて表せ. また \(\text{OP} \cdot \text{OQ} = 1\) であることを示せ.

2. (2)　点 P が直線 \(x+y = 2\) 上を動くとき, 点 Q の軌跡を求めよ.

袋の中に赤と黄と青の玉が \(1\) 個ずつ入っている. 「この袋から玉を \(1\) 個取り出し, 出た玉と同じ色の玉を袋の中に \(1\) 個追加する」という操作を \(N\) 回繰り返した後, 赤の玉が袋の中に \(m\) 個ある確率を \(p _ N (m)\) とする.

1. (1)　連比 \(p _ 3 (1) : p _ 3 (2) : p _ 3 (3) : p _ 3 (4)\) を求めよ.

2. (2)　一般の \(N\) に対し \(p _ N (m) \ ( 1 \leqq m \leqq N+1 )\) を求めよ.

座標空間に \(8\) 点 \[\begin{align} & \text{O} \ (0,0,0) , \quad \text{P} \ (1,0,0) , \quad \text{Q} \ (1,1,0) , \quad \text{R} \ (0,1,0) , \\ & \text{A} \ (0,0,1) , \quad \text{B} \ (1,0,1) , \quad \text{C} \ (1,1,1) , \quad \text{D} \ (0,1,1) \end{align}\] をとり, 線分 BC の中点を M とする. 線分 RD 上の点を N \((0,1,t)\) とし, \(3\) 点 O , M , N を通る平面と線分 PD および線分 PB との交点をそれぞれ K , L とする.

1. (1)　K の座標を \(t\) で表せ.

2. (2)　四面体 OKLP の体積を \(V(t)\) とする. N が線分 RD 上を R から D まで動くとき, \(V(t)\) の最大値と最小値およびそれらを与える \(t\) の値をそれぞれ求めよ.

関数 \(f(x) = (x^2-x) e^{-x}\) について, 次の問いに答えよ. 必要ならば, 任意の自然数 \(n\) に対して \[ \displaystyle\lim _ {x \rightarrow + \infty} x^n e^{-x} = 0 \] が成り立つことを用いてもよい.

1. (1)　\(y = f(x)\) のグラフの変曲点を求め, グラフの概形をかけ.

2. (2)　\(a \gt 0\) とする. 点 \((0,a)\) を通る \(y=f(x)\) のグラフの接線が \(1\) 本だけ存在するような \(a\) の値を求めよ. また, \(a\) がその値をとるとき, \(y=f(x)\) のグラフ, その接線および \(y\) 軸で囲まれた図形の面積を求めよ.

はじめに, A が赤玉を \(1\) 個, B が白玉を \(1\) 個, C が青玉を \(1\) 個持っている. 表裏の出る確率がそれぞれ \(\dfrac{1}{2}\) の硬貨を投げ, 表が出れば A と B の玉を交換し, 裏が出れば B と C の玉を交換する, という操作を考える. この操作を \(n\) 回（ \(n = 1, 2, 3, \cdots\) ）をくり返した後に, A , B , C が赤玉を持っている確率をそれぞれ \(a _ n , b _ n , c _ n\) とおく.

1. (1)　\(a _ 1 , b _ 1 , c _ 1 , a _ 2 , b _ 2 , c _ 2\) を求めよ.

2. (2)　\(a _ {n+1} , b _ {n+1} , c _ {n+1}\) を \(a _ n , b _ n , c _ n\) で表せ.

3. (3)　\(a _ n , b _ n , c _ n\) を求めよ.

解答

(1)

\[\begin{align} a _ 1 & = \underline{\dfrac{1}{2}} , \ b _ 1 = \underline{\dfrac{1}{2}} , \ a _ 1 = \underline{0} , \\ a _ 2 & = \dfrac{1}{2} \cdot \dfrac{1}{2} +\dfrac{1}{2} \cdot \dfrac{1}{2} =\underline{\dfrac{1}{2}} , \\ b _ 2 & = \dfrac{1}{2} \cdot \dfrac{1}{2} =\underline{\dfrac{1}{4}} , \ c _ 2 =\dfrac{1}{2} \cdot \dfrac{1}{2} =\underline{\dfrac{1}{4}} \end{align}\]

(2)

\(n\) 回目の後, A , B , C が赤玉を持った状態から, \(n+1\) 回目で赤玉を誰が持つことになるか, を表す状態遷移は下図のようになる.

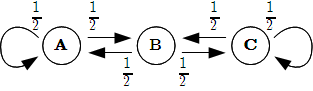
よって \[\begin{align} a _ {n+1} & = \underline{\dfrac{1}{2} a _ n +\dfrac{1}{2} b _ n} \quad ... [1] \\ b _ {n+1} & = \underline{\dfrac{1}{2} a _ n +\dfrac{1}{2} c _ n} \quad ... [2] \\ c _ {n+1} & = \underline{\dfrac{1}{2} b _ n +\dfrac{1}{2} c _ n} \quad ... [3] \end{align}\]

(3)

赤玉は A , B , C の誰かが持っているので \[ a _ n + b _ n + c _ n = 1 \quad ... [4] \] [2] に [4] を用いれば \[\begin{align} b _ {n+1} & = \dfrac{1}{2} -\dfrac{1}{2} b _ n \\ \text{∴} \quad b _ {n+1} -\dfrac{1}{3} & = -\dfrac{1}{2} \left( b _ n -\dfrac{1}{3} \right) \end{align}\] したがって, 数列 \(\left\{ b _ n -\dfrac{1}{3} \right\}\) は, 初項 \(b _ 1 -\dfrac{1}{3} =\dfrac{1}{6}\) , 公比 \(-\dfrac{1}{2}\) の等比数列なので \[\begin{align} b _ n -\dfrac{1}{3} & = \dfrac{1}{6} \left( -\dfrac{1}{2} \right)^{n-1} \\ \text{∴} \quad b _ n & = \underline{\dfrac{1}{3} -\dfrac{1}{3} \left( -\dfrac{1}{2} \right)^n} \end{align}\] これを [1] に代入すると \[\begin{align} a _ {n+1} & = \dfrac{1}{2} a _ n +\dfrac{1}{6} -\dfrac{1}{6} \left( -\dfrac{1}{2} \right)^n \\ \text{∴} \quad a _ {n+1} -\dfrac{1}{3} & -\dfrac{1}{6} \left( -\dfrac{1}{2} \right)^{n+1} = \dfrac{1}{2} \left\{ a _ n -\dfrac{1}{3} -\dfrac{1}{6} \left( -\dfrac{1}{2} \right)^n \right\} \end{align}\] したがって, 数列 \(\left\{ a _ n -\dfrac{1}{3} -\dfrac{1}{6} \left( -\dfrac{1}{2} \right)^n \right\}\) は, 初項 \(a _ 1 -\dfrac{1}{3} +\dfrac{1}{6} \cdot \dfrac{1}{2} =\dfrac{1}{4}\) , 公比 \(\dfrac{1}{2}\) の等比数列なので \[\begin{align} a _ n -\dfrac{1}{3} & -\dfrac{1}{6} \left( -\dfrac{1}{2} \right)^n = \left( \dfrac{1}{2} \right)^{n+1} \\ \text{∴} \quad a _ n & = \underline{\dfrac{1}{3} -\dfrac{1}{3} \left( -\dfrac{1}{2} \right)^{n+1} +\left( \dfrac{1}{2} \right)^{n+1}} \end{align}\] これらと [4] より \[\begin{align} c _ n & = 1-a _ n -b _ n \\ & = 1 -\dfrac{1}{3} +\dfrac{1}{3} \left( -\dfrac{1}{2} \right)^n -\dfrac{1}{3} +\dfrac{1}{3} \left( -\dfrac{1}{2} \right)^{n+1} -\left( \dfrac{1}{2} \right)^{n+1} \\ & =\underline{\dfrac{1}{3} -\dfrac{1}{3} \left( -\dfrac{1}{2} \right)^{n+1} -\left( \dfrac{1}{2} \right)^{n+1}} \end{align}\]

\(xy\) 平面上で \(x\) 座標と \(y\) 座標がともに整数である点を格子点と呼ぶ.

1. (1)　\(y = \dfrac{1}{3} x^2 +\dfrac{1}{2} x\) のグラフ上に無限個の格子点が存在することを示せ.

2. (2)　\(a , b\) は実数で \(a \neq 0\) とする. \(y = ax^2+bx\) のグラフ上に, 点 \((0,0)\) 以外に格子点が \(2\) つ存在すれば, 無限個存在することを示せ.

解答

(1)

\(x = 6n\) （ \(n\) は整数）とおけば \[\begin{align} y & = \dfrac{1}{3} \cdot (6n)^2 +\dfrac{1}{2} \cdot 6n \\ & = 12n^2+3n \end{align}\] これは整数なので, 点 \(( 6n , 12n^2+3n )\) は, \(y=\dfrac{1}{3}x^2 +\dfrac{1}{2}x\) 上の格子点である.
よって, \(n\) は無限にあるので, 格子点も無限個にあるといえる.

(2)

\(y = ax^2+bx\) 上の \(2\) つの格子点を \((x _ 1 , y _ 1) , \ (x _ 2 , y _ 2)\) （ \(x _ 1 , x _ 2\) は互いに異なり \(0\) でない）とおく.
このとき, 条件より \[ \left( \begin{array}{cc} {x _ 1}^2 & x _ 1 \\ {x _ 2}^2 & x _ 2 \end{array} \right) \left( \begin{array}{c} a \\ b \end{array} \right) = \left( \begin{array}{c} y _ 1 \\ y _ 2 \end{array} \right) \] ここで \[ \det \left( \begin{array}{cc} {x _ 1}^2 & x _ 1 \\ {x _ 2}^2 & x _ 2 \end{array} \right) = x _ 1 x _ 2 ( x _ 1 -x _ 2 ) \neq 0 \] なので逆行列 \(\left( \begin{array}{cc} {x _ 1}^2 & x _ 1 \\ {x _ 2}^2 & x _ 2 \end{array} \right)^{-1}\) が存在し \[ \left( \begin{array}{c} a \\ b \end{array} \right) = \dfrac{1}{x _ 1 x _ 2 ( x _ 1 -x _ 2 )} \left( \begin{array}{cc} x _ 2 & -x _ 1 \\ -{x _ 2}^2 & {x _ 1}^2 \end{array} \right) \left( \begin{array}{c} y _ 1 \\ y _ 2 \end{array} \right) \] \(x _ 1 , x _ 2 , y _ 1 , y _ 2\) はすべて整数なので, \(a , b\) はともに有理数である.
そこで, \(a =\dfrac{p _ 1}{q _ 1}\) , \(b =\dfrac{p _ 2}{q _ 2}\) （ \(p _ 1 , p _ 2 , q _ 1 , q _ 2\) は整数）とおく.
\(x = q _ 1 q _ 2 n\) （ \(n\) は整数）とおけば \[\begin{align} y & = \dfrac{p _ 1}{q _ 1} \cdot (q _ 1 q _ 2 n)^2 +\dfrac{p _ 2}{q _ 2} \cdot q _ 1 q _ 2 n \\ & = p _ 1 q _ 1 {q _ 2}^2 n^2 +p _ 2 q _ 1 n \end{align}\] これは整数なので, 点 \(( q _ 1 q _ 2 n , p _ 1 q _ 1 {q _ 2}^2 n^2 +p _ 2 q _ 1 n )\) は, \(y = ax^2 +bx\) 上の格子点である.
よって, \(n\) は無限にあるので, 格子点も無限個にあるといえる.

\(a\) を正の定数とし, \(xy\) 平面上の曲線 \(C\) の方程式を \(y = x^3 -a^2x\) とする.

1. (1)　\(C\) 上の点 A \(( t, t^3 -a^2t )\) における \(C\) の接線を \(\ell\) とする. \(\ell\) と \(C\) で囲まれた図形の面積 \(S(t)\) を求めよ. ただし, \(t\) は \(0\) でないとする.

2. (2)　\(b\) を実数とする. \(C\) の接線のうち \(xy\) 平面上の点 B \(( 2a , b )\) を通るものの本数を求めよ.

3. (3)　\(C\) の接線のうち点 B \(( 2a , b )\) を通るものが \(2\) 本のもの場合を考え, それらの接線を \(\ell _ 1 , \ell _ 2\) とする. ただし, \(\ell _ 1\) と \(\ell _ 2\) はどちらも原点 \((0,0)\) は通らないとする. \(\ell _ 1\) と \(C\) で囲まれた図形の面積を \(S _ 1\) とし, \(\ell _ 2\) と \(C\) で囲まれた図形の面積を \(S _ 2\) とする. \(S _ 1 \geqq S _ 2\) として, \(\dfrac{S _ 1}{S _ 2}\) の値を求めよ.

\(f _ 0 (x) = x e^x\) として, 正の整数 \(n\) に対して, \[ f _ n (x) = \displaystyle\int _ {-x}^x f _ {n-1} (t) \, dt +f' _ {n-1} (x) \] により実数 \(x\) の関数 \(f _ n (x)\) を定める.

1. (1)　\(f _ 1 (x)\) を求めよ.

2. (2)　\(g(x) = \displaystyle\int _ {-x}^x (at+b) e^t \, dt\) とするとき, 定積分 \(\displaystyle\int _ {-c}^c g(x) \, dx\) を求めよ. ただし, 実数 \(a , b , c\) は定数とする.

3. (3)　正の整数 \(n\) に対して, \(f _ {2n} (x)\) を求めよ.