\(2\) 次の正方行列 \(A\) を \(A = \left( \begin{array}{cc} -\dfrac{1}{\sqrt{2}} & -\dfrac{1}{\sqrt{2}} \\ \dfrac{1}{\sqrt{2}} & -\dfrac{1}{\sqrt{2}} \end{array} \right)\) で定める.
\(n = 1, 2, 3, \cdots\) に対して, 点 \(\text{P} {} _ n \ \left( x _ n , y _ n \right)\) を関係式
\[
\left( \begin{array}{c} x _ n \\ y _ n \end{array} \right) = A \left( \begin{array}{c} x _ {n-1} \\ y _ {n-1} \end{array} \right) + \left( \begin{array}{c} 1 \\ 0 \end{array} \right) \quad ( n = 1, 2, 3, \cdots ) \ .
\]
で定める. ただし, \(x _ 0 = 1\) , \(y _ 0 = 0\) とする.
【 解 答 】
(1)
原点中心に \(\theta\) だけ回転する移動を表す行列を \(R( \theta )\) とおくと
\[
R( \theta ) = \left( \begin{array}{cc} \cos \theta & -\sin \theta \\ \sin \theta & \cos \theta \end{array} \right) \ .
\]
条件より
\[
A = R \left( \dfrac{3 \pi}{4} \right) \ .
\]
なので
\[
A^4 = R( 3 \pi ) = \underline{\left( \begin{array}{cc} -1 & 0 \\ 0 & -1 \end{array} \right)} \ .
\]
(2)
\[\begin{align}
\left( E -A^{n+1} \right) & (E-A)^{-1} \\
& = \left( E +A + \cdots +A^n \right) (E-A) (E-A)^{-1} \\
& = \textstyle\sum\limits _ {k=0}^n A^k \ .
\end{align}\]
なので, \(n = 0 , 1 , 2 , \cdots\) に対して
\[
\left( \begin{array}{c} x _ n \\ y _ n \end{array} \right) = \textstyle\sum\limits _ {k=0}^n A^k \left( \begin{array}{c} 1 \\ 0 \end{array} \right) \quad ... [ \text{A} ] \ .
\]
が成り立つことを示せばよい.
以下では, 数学的帰納法を用いてこれを示す.
1* \(n = 0\) のとき, 条件より [A] は成立する.
2* \(n = \ell \ ( \ell \geqq 0 )\) のとき, [A] が成立すると仮定すると
\[\begin{align}
\left( \begin{array}{c} x _ {\ell +1} \\ y _ {\ell +1} \end{array} \right) & = A \left( \begin{array}{c} x _ {\ell} \\ y _ {\ell} \end{array} \right) +\left( \begin{array}{c} 1 \\ 0 \end{array} \right) \\
& = A \textstyle\sum\limits _ {k=0}^{\ell} A^k \left( \begin{array}{c} 1 \\ 0 \end{array} \right) +\left( \begin{array}{c} 1 \\ 0 \end{array} \right) \\
& = \left( \textstyle\sum\limits _ {k=1}^{\ell +1} A^k +E \right) \left( \begin{array}{c} 1 \\ 0 \end{array} \right) \\
& = \textstyle\sum\limits _ {k=0}^{\ell +1} A^k \left( \begin{array}{c} 1 \\ 0 \end{array} \right) \ .
\end{align}\]
ゆえに, \(n = \ell +1\) のときも [A] が成立する.
以上より, 題意は示された.
(3)
\(B _ n = \textstyle\sum\limits _ {k=0}^n A^k\) とおく.
(1) の結果より
\[\begin{align}
B _ 7 & = E+A+A^2+A^3-E-A-A^2-A^3 \\
& = O \ .
\end{align}\]
なので
\[\begin{align}
B _ {n+8} & = A^{n+1} B _ 7 +B _ n \\
& = B _ n \ .
\end{align}\]
ゆえに, (2) の結果より
\[
\left( \begin{array}{c} x _ {n+8} \\ y _ {n+8} \end{array} \right) = \left( \begin{array}{c} x _ {n} \\ y _ {n} \end{array} \right) \quad ... [1] \ .
\]
したがって, 最大値をとる \(\text{P} {} _ n\) は \(\text{P} {} _ 0 , \text{P} {} _ 1 , \cdots , \text{P} {} _ 7\) の \(8\) 個のいずれかである.
さらに, \(n = 1 , 2 , \cdots\) について
\[\begin{align}
B _ n -B _ {n-1} & = A^n = R \left( \dfrac{3n \pi}{4} \right) \\
\text{∴} \quad \overrightarrow{\text{P} {} _ {n-1} \text{P} {} _ {n}} & = \left( \begin{array}{c} \cos \frac{3n \pi}{4} \\ \sin \frac{3n \pi}{4} \end{array} \right) \ .
\end{align}\]
したがって, \(\text{P} {} _ 0 , \text{P} {} _ 1 , \cdots , \text{P} {} _ 7\) は下図のように, 正 \(8\) 角形をなす.
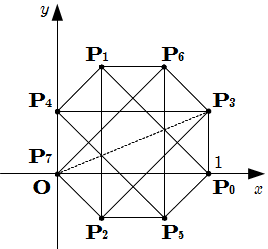
ここで, 原点 O からの距離が最大であるのは \(\text{P} {} _ 3\) なので
[1] に注意すれば, 求める \(n\) は
\[
n =\underline{8k+3} \quad ( k = 0 , 1 , 2 , \cdots ) \ .
\]
« 解答を隠す



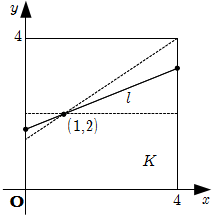 \[
L = 4 \sqrt{a^2+1}
\]
この区間では \(L\) は単調増加である.
\[
L = 4 \sqrt{a^2+1}
\]
この区間では \(L\) は単調増加である.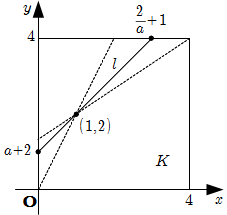 \[\begin{align}
L & = \sqrt{(a+2)^2 +\left( \dfrac{2}{a} +1 \right)^2} \\
& =(a+2) \sqrt{1+ \dfrac{1}{a^2}} \\
& = \left( 1+\dfrac{2}{a} \right) \sqrt{a^2+1}
\end{align}\]
したがって
\[\begin{align}
\dfrac{dL}{da} & = -\dfrac{2 \sqrt{a^2+1}}{a^2} +\dfrac{a+2}{a} \cdot \dfrac{a}{\sqrt{a^2+1}} \\
& = \dfrac{-2 ( a^2+1 ) +a^2 (a+2)}{a^2 \sqrt{a^2+1}} \\
& = \dfrac{a^3-2}{a^2 \sqrt{a^2+1}}
\end{align}\]
\(\dfrac{dL}{da} = 0\) をとくと
\[
a = 2^{\frac{1}{3}}
\]
\[\begin{align}
L & = \sqrt{(a+2)^2 +\left( \dfrac{2}{a} +1 \right)^2} \\
& =(a+2) \sqrt{1+ \dfrac{1}{a^2}} \\
& = \left( 1+\dfrac{2}{a} \right) \sqrt{a^2+1}
\end{align}\]
したがって
\[\begin{align}
\dfrac{dL}{da} & = -\dfrac{2 \sqrt{a^2+1}}{a^2} +\dfrac{a+2}{a} \cdot \dfrac{a}{\sqrt{a^2+1}} \\
& = \dfrac{-2 ( a^2+1 ) +a^2 (a+2)}{a^2 \sqrt{a^2+1}} \\
& = \dfrac{a^3-2}{a^2 \sqrt{a^2+1}}
\end{align}\]
\(\dfrac{dL}{da} = 0\) をとくと
\[
a = 2^{\frac{1}{3}}
\]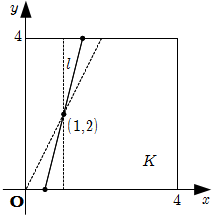 \[
L = 4 \sqrt{1+\dfrac{1}{a^2}}
\]
この区間では \(L\) は単調減少である.
\[
L = 4 \sqrt{1+\dfrac{1}{a^2}}
\]
この区間では \(L\) は単調減少である.